
题目列表(包括答案和解析)
8.判断函数f(x)=的奇偶性.
[解析] ①当x>0时,-x<0,
则f(-x)=2·(-x)-3=-(2x+3)=-f(x)
②当x<0时,-x>0
f(-x)=-2x+3=-(2x-3)=-f(x)
③当x=0时,f(0)=0
即f(-x)=-f(x).
∴f(x)是奇函数.

7.判断下列函数是否具有奇偶性:
(1)f(x)=x+1;
(2)f(x)=x2+3x,x∈[-4,4);
(3)f(x)=x2+1,x∈[-6,-2]∪[2,6];
[解析] (1)函数f(x)=x+1的定义域为实数集R,
当x∈R时,-x∈R.
因为f(-x)=-x+1=-(x-1),-f(x)=-(x+1),
即f(-x)≠-f(x),f(-x)≠f(x).
所以函数f(x)=x+1既不是奇函数又不是偶函数.
(2)因为函数的定义域关于坐标原点不对称,即存在-4∈
[-4,4),而4∉[-4,4).
所以函数f(x)=x3+3x,
x∈[-4,4)既不是奇函数又不是偶函数.
(3)函数f(x)=x2+1的定义域为[-6,-2]∪[2,6],当x∈[-6,-2]时,-x∈[2,6].
因为f(-x)=(-x)2+1=x2+1=f(x),
所以函数f(x)=x2+1,x∈[-6,-2]∪[2,6]是偶函数.
6.已知函数y=f(x)为奇函数,若f(3)-f(2)=1,则f(-2)-f(-3)=________.
[解析] 函数y=f(x)为奇函数,故f(-x)=-f(x),则f(-2)-f(-3)=-f(2)+f(3)=1.
[答案] 1
5.设函数f(x)=为奇函数,则a=________.
[解析] f(-x)=,又f(x)为奇函数,故f(x)=-f(-x),
即=,所以=,从而有a+1=-(a+1),即a=-1.
[答案] -1
4.对于定义域为R的奇函数f(x),下列结论成立的是( )
A.f(x)-f(-x)>0 B.f(x)-f(-x)≤0
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
[解析] f(-x)=-f(x),
则f(x)·f(-x)=-f2(x)≤0,故选C.
[答案] C
3.函数y=(x+2)(x-a)是偶函数,则a=( )
A.2 B.-2
C.1 D.-1
[解析] 结合选项,a=2时,f(x)=x2-4是偶函数,故选A.
[答案] A
2.下列图象中能表示具有奇偶性的函数图象的可能是( )

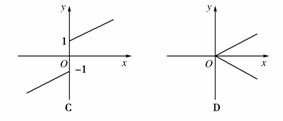
[解析] 图象关于原点或y轴对称的函数具有奇偶性.选项A,D中的图形关于原点或y轴均不对称,故排除;选项C中的图形虽然关于坐标原点对称,但是过(0,-1)和(0,1)两点,这说明当x=0时,y=±1,不符合函数的概念,不是函数的图象,故排除;选项B中图形关于y轴对称,是偶函数.故选B.
[答案] B
1.如图

是一个由集合A到集合B的映射,这个映射表示的是( )
A.奇函数而非偶函数
B.偶函数而非奇函数
C.奇函数且偶函数
D.既不是奇函数也不是偶函数
[解析] 因为f(x)=0,x∈{-2,2},
满足f(-x)=±f(x).
所以该映射表示的既是奇函数又是偶函数.
[答案] C
20.(1)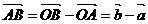
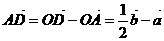
 设
设 ,
,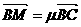 ,
,


得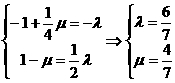
 .
.
(2) ,
,
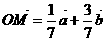
又 三点共线,
三点共线, ,由
,由 存在唯一一个实数
存在唯一一个实数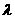 使
使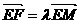 而
而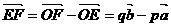

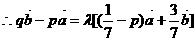
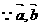 不共线
不共线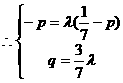
整理得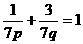 .
.
19.设交点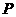 的坐标为
的坐标为
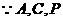 共线
共线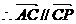
 ,
,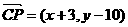

 …………(1)
…………(1)
又 共线
共线
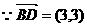 ,
,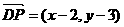
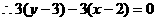
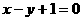 …………(2)
…………(2)
由(1)(2)得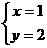
 交点
交点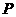 为
为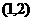 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com