2．如果lgx=lga+3lgb－5lgc，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．x=a+3b－c　　　　　 B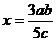． 　　　　　 C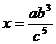．　　 　　 D．x=a+b³－c³

1．对数式中，实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

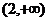A．　　　　　　　 B．(2,5)　　　　　　　　　 C．　　　　　　　 D．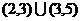

9．(10分)函数y＝log(x²－ax+a)在(－∞，)上单调递增，求a的取值范围．

[解析]　∵f(x)＝log(x²－ax+a)在(－∞，)上单调递增，

∴令g(x)＝x²－ax+a，g(x)＝²+a－，

在(－∞，)上单调递减．

∴欲使g(x)在(－∞，)上单调递减，需有

∴2≤a≤2+2.

8．求证：函数f(x)＝lg(－1<x<1)是奇函数且是减函数．

[证明]　设x∈(－1,1)

f(－x)＝lg＝lg^－1

＝－lg＝－f(x)，

∴f(x)为奇函数．

设x₁，x₂∈(－1,1)，且x₁<x₂，

设t₁＝，t₂＝，

则t₁－t₂＝－

＝

＝.

∵－1<x₁<x₂<1，∴t₁－t₂>0.

∴t₁>t₂，∴lg t₁>lg t₂.

∴f(x₁)>f(x₂)，∴f(x)为减函数．

7．比较下列各组中，两对数值的大小．

(1)log₂3.4和log₂7.5；

(2)log₃4和log₄3；

(3)log_0.5π和log_0.60.8.

[解析]　(1)∵y＝log₂x为递增函数，又3.4<7.5，

∴log₂3.4<log₂7.5.

(2)∵log₃4>log₃3＝1，log₄3<log₄4<1.

∴log₃4>log₄3.

(3)∵log_0.5π<log_0.51＝0，log_0.60.8>0，

∴log_0.5π<log_0.60.8.

6．已知log_0.6(x+2)>log_0.6(1－x)，则实数x的取值范围是________．

[解析]　∵y＝log_0.6x在(0，+∞)是减函数

∴∴－2<x<－.

[答案]　(－2，－)

5．如果函数y＝log_ax对于区间[2，+∞)上的每一个x值都有y>1，则实数a的取值范围为________．

[解析]　已知y>1，即log_ax>1，又x∈[2，+∞)，故a>1，要使得对于区间[2，+∞)上的每一个x值都有y>1，等价于函数y＝log_ax在区间[2，+∞)上的最小值log_a2>1，由此得a<2.故a的取值范围为1<a<2.

[答案]　1<a<2

4．设a>1，函数f(x)＝log_ax在区间[a,2a]上的最大值与最小值之差为，则a等于(　)

A.　 B．2

C．2　 D．4

[解析]　因为a>1，所以函数f(x)＝log_ax在区间[a,2a]上是增函数，于是log_a(2a)－log_aa＝，即log_a2＝，所以a＝4.故选D.

[答案]　D

3．已知函数f(x)＝log_a(x－1)(a>0，a≠1)在区间(1,2)上满足f(x)<0，则函数f(x)为(　)

A．增函数　 B．减函数

C．先增后减　 D．先减后增

[解析]　已知1<x<2，则0<x－1<1，此时f(x)<0，根据对数函数的图象知a>1.所以函数f(x)为增函数．故选A.

[答案]　A

2．若log_a2<1，则(　)

A．a∈(1,2)　 B．a∈(0,1)∪(2，+∞)

C．a∈(0,1)∪(1,2)　 D．a∈(0，)

[解析]　①若0<a<1，则log_a2<0；

②若a>1，log_a2<log_aa

∴a<2，

∴1<a<2.故选A.

[答案]　A