6.对于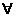x₁，x₂∈R(注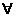：表示“任意”)，恒有f(x₁)·f(x₂)=f(x₁+x₂)成立，且f(1)=，则f(6)=(　 )

A．2　　 B．4　　　　　　 C．　　　　 D．8

5.函数y=f(x)的图象与y=2^1-x的图象关于直线x=1对称，则f(x)为(　 )

A．y=2^x-1

B．y=2^x+1

C．y=2^x-2

D．y=2^2-x

4.若指数函数y=a^x经过点(-1，3)，则a等于(　 )

A．3　　　　　　 B．　　　　　 C．2　　　　　　 D．

3.若函数y=f(x)的图象与y=2^-x的图象关于y轴对称，则f(3)=(　 )

A．8　　　　　　 B．4　　　　　　 C．　　　　　 D．

l.设指数函数C₁：y=a^x，C₂：y=b^x，C₃：y=c^x的图象如图，则(　 )

A．0<c<1<b<a

B．0<a<1<b<c

C．c<b<a

D．0<c<1<a<b

2.函数y=a^x-1(a>0，a≠1)过定点，则这个定点是(　 )

A．(0，1)　　　 B．(1，2)　　　 C．(-1，0.5)　　　 D．(1，1)

19.低压燃煤气体是通过管道输送的．在固定的压力差下，当燃煤气体通过圆形管道时，其流量速率v(cm³／s)与管道的直径(内径)d(cm)的四次方成正比．

(1)若燃煤气体在直径为6 cm的管道中，流量速率为400 cm³／s，求该燃煤气体通过直径为d的管道时，其流量速率的表达式；

(2)要向某居民小区每小时供给36 m³。燃煤气体，输送燃煤气体管道内径至少为多少?

答案：(1)设比例常数为k，则v=kd⁴，当d=6 cm时，v=400cm³／s，∴400=k6⁴，k=, ∴v=d⁴

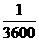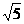(2)∵v=36××10⁶=10 000(cm³/s), ∴10 000=，即直径为6cm

18.完成下列各题：

(1)确定x的值，使不等式a^2x-1>a^3x(a>0，a≠1)成立；

(2)已知函数f(x)=2x-1，g(x)=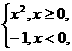求f[g(x)]的表达式．

答案：(1)①当0<a<1时，x>-1；②当a>1时，x<-1

(2)当x≥0时，f[g(x)]=f(x²)=2x²-1；当x<0时，f[g(x)]=f(-1)=-3

17.某IP产品原来每年市场需求量为a，在今后n年内，估计市场需求量平均每年比上一年增加p%，写出市场需求量随年数x(1≤x≤n，x∈N*)变化的函数解析式f(x)，并求当p=0.2时，经过多少年市场的需求量增加1成?若p≤0.3时，(1+p%)^x≈1+xp%，试计算结果并作比较．

答案：函数y=a(1+p%)^x(1≤x≤n，x∈N*)，当p=0.2时，a(1+0.002)^x=1.1a，从而有：x=log_l.002 l.1≈48，当p≤0.3时，a(1+0.002)^x≈a(1+0.002x)=1.1ax=50，绝对误差是50-48=2

16.设函数f(x)=log_π(2+x)和函数g(x)=log_π(2一x)，令函数F(x)=f(x)+g(x)．(1)求函数F(x)的定义域；(2)判断函数F(x)奇偶性，并说明理由；(3)判断函数F(x)的单调性，并说明理由．

答案：(1)定义域：{x|-2<x<2}

(2)∵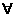x∈{x|-2<x<2)，f(-x)=log_π(2-x)+log(2+x)=F(x)，∴F(x)是偶函数

(3)∵F(x)=log_π(4-x²)，∴F(x)在(-2，0]上是增函数，F(x)在[0，2)上是减函数

15.证明幂函数f(x)=在(-∞，+∞)上是增函数．

答案：设x₁<x₂时，f(x₁)-f(x₂)== ，∵x₁<x₂, ∴x₁-x₂<0,又∵()²+()²>0，∴f(x₁)-f(x₂)<0，即f(x₁)<f(x₂)，∴f(x)在R上是增函数