
题目列表(包括答案和解析)
4、在等比数列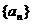 中,已知
中,已知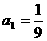 ,
,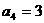 ,则该数列前5项的积为( )
,则该数列前5项的积为( )
A. B.3
C.1
D.
B.3
C.1
D.
3、已知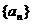 是等比数列,且
是等比数列,且 ,
, ,那么
,那么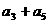 的值是(
)
的值是(
)
A.5 B.6 C.7 D.25
2、已知 ,
, ,
, ,
,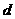 是公比为2的等比数列,则
是公比为2的等比数列,则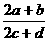 等于(
)
等于(
)
A.1
B. C.
C.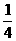 D.
D.
1、 是
是 ,
, ,
, 成等比数列的(
)
成等比数列的(
)
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
9.(10分)在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障,这是一条10 km长的线路,如何迅速查出故障所在?
如果沿着线路一小段一小段查找,困难很多,每查一个点要爬一次电线杆子,10 km长,大约有200多根电线杆子呢!想一想,维修线路的工人师傅怎样工作最合理?
[解析] 如图

他首先从点C查,用随身带的话机向两端测试时,发现AC段正常,断定故障在BC段,再查BC段中点D,这次发现BD段正常,可见故障在CD段,再查CD中点E.
这样每查一次,就可以把待查的线路长度缩减一半,故经过7次查找,即可将故障发生的范围缩小到50 m-100 m之间,即一两根电线杆附近.
8.求方程ln x+x-3=0在(2,3)内的根(精确到0.1).
[解析] 令f(x)=ln x+x-3,即求函数f(x)在(2,3)内的零点.
用二分法逐步计算.列表如下:
|
区间 |
中点 |
中点函数值 |
|
[2,3] |
2.5 |
0.416 3 |
|
[2,2.5] |
2.25 |
0.060 9 |
|
[2,2.25] |
2.125 |
-0.121
2 |
|
[2.125,2.25] |
2.187 5 |
-0.029
7 |
|
[2.187 5,2.25] |
|
|
由于区间[2.187 5,2.25]的长度2.25-2.187 5=0.062 5<0.1,所以其两个端点的近似值2.2就是方程的根.

7.求方程2x3+3x-3=0的一个近似解(精确度0.1).
[解析] 设f(x)=2x3+3x-3,经试算,f(0)=-3<0,f(1)=2>0,所以函数在(0,1)内存在零点,即方程2x3+3x-3=0在(0,1)内有实数解,取(0,1)的中点0.5,经计算f(0.5)<0,又f(1)>0,所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的一个实数解所在的区间,如下表:
|
(a,b) |
(a,b)的中点 |
f(a) |
f(b) |
f |
|
(0,1) |
0.5 |
f(0)<0 |
f(1)>0 |
f(0.5)<0 |
|
(0.5,1) |
0.75 |
f(0.5)<0 |
f(1)>0 |
f(0.75)>0 |
|
(0.5,0.75) |
0.625 |
f(0.5)<0 |
f(0.75)>0 |
f(0.625)<0 |
|
(0.625,0.75) |
0.687 5 |
f(0.625)<0 |
f(0.75)>0 |
f(0.687 5)<0 |
因为|0.687 5-0.75|=0.062 5<0.1,所以方程2x3+3x-3=0的精确度为0.1的一个近似解可取为0.75.
6.用二分法求方程x3-2x-5=0在区间[2,3]内的实数根时,取区间中间x0=2.5,那么下一个有根区间是________.
[解析] ∵f(2)<0,f(2.5)>0,
∴下一个有根区间是(2,2.5).
[答案] (2,2.5)
5.用二分法求函数y=f(x)在区间(2,4)上的近似解,验证f(2)·f(4)<0,给定精确度ε=0.01,取区间(2,4)的中点x1==3,计算得f(2)·f(x1)<0,则此时零点x0∈________(填区间).
[解析] 由f(2)·f(3)<0可知.
[答案] (2,3)
4.函数f(x)=ex-的零点所在的区间是( )
A. B.
C. D.
[解析] f()=-2<0,
f(1)=e-1>0,
∵f()·f(1)<0,
∴f(x)的零点在区间内,故选B.
[答案] B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com