
题目列表(包括答案和解析)
2.函数f(x)=(a2-1)x在R上是减函数,则a的取值范围是( )
(A)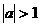 (B)
(B) (C)a<
(C)a<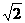 (D)1<
(D)1<
1.(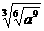 )4(
)4( )4等于( )
)4等于( )
(A)a16 (B)a8 (C)a4 (D)a2
9.(10分)已知函数f(x)=3x+3-x.
(1)判断函数的奇偶性;
(2)求函数的单调增区间,并证明.
[解析] (1)f(-x)=3-x+3-(-x)=3-x+3x=f(x)且x∈R,
∴函数f(x)=3x+3-x是偶函数.
(2)由(1)知,函数的单调区间为(-∞,0]及[0,+∞),且[0,+∞)是单调增区间.
现证明如下:
设0≤x1<x2,则f(x1)-f(x2)=3x1+3-x1-3x2-2-x2
=3x1-3x2+-=3x1-3x2+
=(3x2-3x1)·.
∵0≤x1<x2,∴3x2>3x1,3x1+x2>1,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数在[0,+∞)上单调递增,
即函数的单调增区间为[0,+∞).
8.已知a>0且a≠1,讨论f(x)=a-x2+3x+2的单调性.
[解析] 设u=-x2+3x+2=-2+,
则当x≥时,u是减函数,当x≤时,u是增函数.
又当a>1时,y=au是增函数,当0<a<1时,y=au是减函数,
所以当a>1时,原函数f(x)=a-x2+3x+2在上是减函数,在上是增函数.
当0<a<1时,原函数f(x)=a-x2+3x+2在上是增函数,在上是减函数.

7.根据下列条件确定实数x的取值范围:<1-2x(a>0且a≠1).
[解析] 原不等式可以化为a2x-1>a,因为函数y=ax(a>0且a≠1)当底数a大于1时在R上是增函数;当底数a大于0小于1时在R上是减函数,
所以当a>1时,由2x-1>,解得x>;
当0<a<1时,由2x-1<,解得x<.
综上可知:当a>1时,x>;当0<a<1时,x<.
6.下列空格中填“>、<或=”.
(1)1.52.5________1.53.2,(2)0.5-1.2________0.5-1.5.
[解析] (1)考察指数函数y=1.5x.
因为1.5>1,所以y=1.5x在R上是单调增函数.
又因为2.5<3.2,所以1.52.5<1.53.2.
(2)考察指数函数y=0.5x.
因为0<0.5<1,所以y=0.5x在R上是单调减函数.
又因为-1.2>-1.5,所以0.5-1.2<0.5-1.5.
[答案] <,<
5.设a>0,f(x)=+(e>1),是R上的偶函数,则a=________.
[解析] 依题意,对一切x∈R,都有f(x)=f(-x),
∴+=+aex,
∴(a-)(ex-)=0.
∴a-=0,即a2=1.
又a>0,∴a=1.
[答案] 1
4.如果函数f(x)=(1-2a)x在实数集R上是减函数,那么实数a的取值范围是( )
A.(0,) B.(,+∞)
C.(-∞,) D.(-,)
[解析] 根据指数函数的概念及性质求解.
由已知得,实数a应满足,解得,
即a∈(0,).故选A.
[答案] A
3.设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当x≥1时,f(x)=3x-1,则有( )
A.f()<f()<f()
B.f()<f()<f()
C.f()<f()<f()
D.f()<f()<f()
[解析] 因为f(x)的图象关于直线x=1对称,所以f()=f(),f()=f(),因为函数f(x)=3x-1在[1,+∞)上是增函数,所以f()>f()>f(),即f()<f()<f().故选B.
[答案] B
2.若2a+1<3-2a,则实数a的取值范围是( )
A. B.
C.(-∞,1) D.
[解析] 函数y=x在R上为减函数,
∴2a+1>3-2a,∴a>.故选A.
[答案] A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com