3.函数y=的定义域是(　 )

A．{2}

B．{1，2}

C．{x|x≤-2}

D．

2.下列函数表示偶函数的是(　 )

A．y=

B．y=x³

C．y=x+1

D．y=x²(-1<x≤1)

1.下列函数中与函数y=x-1相同的是(　 )

A．y=()²

B．y=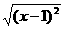

C．y=

D．y=

9．(10分)根据总的发展战略，第二阶段，我国工农业生产总值从2000年到2020年间要翻两番，问这20年间，每年平均增长率至少要多少，才能完成这一阶段构想？

[解析]　设平均每年增长率为x.

从2000年到2020年共21年，若记2000年工农业总产值为1，则2001,2002,2003，……的年总产值分别为(1+x)，(1+x)²，(1+x)³，…，第n年为(1+x)^n－1.

根据题意，有(1+x)²⁰＝2²，两边取对数得20lg(1+x)＝2lg2，

即lg(1+x)＝lg2，

∴lg(1+x)＝0.030 1，

∴1+x≈1.072，

∴x≈0.072＝7.2%.

即平均每年增长7.2%，即可完成第二阶段的任务．

8．依法纳税是每个公民应尽的义务，国家征收个人工资、薪金所得税是分段计算的：总收入不超过2 000元的，免征个人工资、薪金所得税；超过2 000元部分需征税，设全月纳税所得额(所得额指工资、薪金中应纳税的部分)为x，x＝全月总收入－2 000元，税率如表所示：

(1)若应纳税额为f(x)，试用分段函数表示1-3级纳税额f(x)的计算公式；

(2)某人2008年10月份工资总收入为4 200元，试计算这个人10月份应纳个人所得税多少元？

[解析]　(1)第1级：

f(x)＝x·5%＝0.05x

第2级：

f(x)＝500×5%+(x－500)×10%

＝0.1x－25

第3级：

f(x)＝500×5%+1 500×10%+(x－2 000)×15%＝0.15x－125.

∴f(x)＝.

(2)这个人10月份的纳税所得额为

4 200－2 000＝2 200(元)，

∴f(2 200)＝2 200×0.15－125

＝205(元)，

即这个人10月份应纳个人所得税205元．

7．某城市现有人口总数为100万人，如果年自然增长率为1.2%，试解答下面的问题：

(1)写出该城市人口总数y(万人)与年份x(年)的函数关系式；

(2)计算10年以后该城市人口总数(精确到0.1万人)；(1.012¹⁰＝1.127)

[解析]　(1)1年后该城市人口总数为

y＝100+100×1.2%＝100×(1+1.2%)．

2年后该城市人口总数为

y＝100×(1+1.2%)+100×(1+1.2%)×1.2%

＝100×(1+1.2%)².

3年后该城市人口总数为

y＝100×(1+1.2%)²+100×(1+1.2%)²×1.2%

＝100×(1+1.2%)²×(1+1.2%)

＝100×(1+1.2%)³.

…

x年后该城市人口总数为

y＝100×(1+1.2%)^x(x∈N)．

(2)10年后人口数为100×(1+1.2%)¹⁰≈112.7(万)．

6．某商品前两年每年递增20%，后两年每年递减20%，则四年后的价格与原来的价格比较，变化情况是________．

[解析]　设原来商品价格为1个单位，

则1×(1+20%)²×(1－20%)²

＝0.921 6＝92.16%，

∴减少了7.84%.

[答案]　减少了7.84%

5．某种病毒经30分钟繁殖为原来的2倍，且知病毒的繁殖规律为y＝e^kt(其中k为常数，t表示时间，单位：小时，y表示病毒个数)，则k＝________，经过5小时，1个病毒能繁殖为________个．

[解析]　当t＝0.5时，y＝2，∴2＝ek，

∴k＝2ln2，∴y＝e^2tln2，当t＝5时，

∴y＝e^10ln2＝2¹⁰＝1 024.

[答案]　2ln2　1 024

4．某厂原来月产量为a，一月份增产10%，二月份比一月份减产10%，设二月份产量为b，则(　)

A．a＝b　 B．a>b

C．a<b　 D．无法比较a、b的大小

[解析]　∵b＝a(1+10%)(1－10%)，

∴b＝a[1－(10%)²]＝a，

∴b＝a×，

∴a>b.故选B.

[答案]　B

3．拟定从甲地到乙地通话m分钟的电话费f(m)＝1.06·(0.50×[m]+1)，其中m>0，[m]是大于或等于m的最小整数(如[3]＝3，[3.7]＝4，[5.1]＝6)，则从甲地到乙地通适时间为5.5分钟的通话费为(　)

A．3.71　 B．3.97

C．4.24　 D．4.77

[解析]　5.5分钟的通话费为

f(5.5)＝1.06×(0.50×[5.5]+1)＝1.06×(0.50×6+1)＝1.06×4＝4.24，故选C.

[答案]　C