12.求函数y=4^-x-2^-x+1,x∈［-3,2］的最大值和最小值.

解：设2^-x=t,由x∈［-3,2］得t∈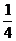［,8］,于是y=t²-t+1=(t-)²+.

当t=时,y有最小值.

这时x=1.

当t=8时,y有最大值57.

这时x=-3.

11.设有两个命题:(1)关于x的不等式x²+2ax+4>0对一切x∈R恒成立;(2)函数f(x)=-(5-2a)^x是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a的取值范围是_________________.

答案：(-∞,-2)

解析：(1)为真命题Δ=(2a)²-16<0-2<a<2.

(2)为真命题5-2a>1a<2.

若(1)假(2)真,则a∈(-∞,-2].

若(1)真(2)假,则a∈(-2,2)∩［2,+∞］=.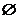

故a的取值范围为(-∞,-2).

10.当x∈［-1,1］时,函数f(x)=3^x-2的值域为__________________.

答案：［-,1］

解析：f(x)在［-1,1］上单调递增.

9.函数y=a^x与y=-a^-x(a>0,a≠1)的图象(　　 )

A.关于x轴对称　　　　　　　　　　 B.关于y轴对称

C.关于原点对称　　　　　　　　　　 D.关于直线y=-x对称

答案：C

解析：可利用函数图象的对称性来判断两图象的关系.

8.若定义运算a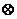b=则函数f(x)=3^x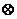3^-x的值域为(　　 )

A.(0,1]　　　　　　　 B.［1,+∞)　　　 C.(0,+∞)　　　　　 D.(-∞,+∞)

答案：A

解析：当3^x≥3^-x,即x≥0时,f(x)=3^-x∈(0,1］;

当3^x<3^-x,即x<0时,f(x)=3^x∈(0,1).

∴f(x)=值域为(0,1).

7.已知函数f(x)=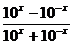.证明f(x)在R上是增函数.

证明：∵f(x)=,

设x₁<x₂∈R,

则f(x₁)-f(x₂)=.

∵y=10^x是增函数,

∴<0.

而+1>0,+1>0,

故当x₁<x₂时,f(x₁)-f(x₂)<0,

即f(x₁)<f(x₂).

所以f(x)是增函数.

能力提升　 踮起脚,抓得住!

6.函数y=a^x-3+4(a>0且a≠1)的反函数的图象恒过定点__________________.

答案：(5,3)

解析：因y=a^x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a^x-3+4的图象,易知恒过定点(3,5).

故其反函数过定点(5,3).

5.设f(x)=4^x-2^x+1,则f^-1(0)=__________________.

答案：1

解析：令f^-1(0)=a,则f(a)=0即有4^a-2·2^a=0.?

2^a·(2^a-2)=0,而2^a>0,

∴2^a=2得a=1.

4.设a=,b=,c=,则a、b、c的大小关系是(　　 )

A.c<a<b　　　　　　　 B.c<b<a　　　　 C.b<a<c　　　　　 D.b<c<a

答案：B

解析：a==b,

b==c.

∴a>b>c.

3.设指数函数f(x)=a^x(a>0且a≠1),则下列等式中不正确的是(　　 )

A.f(x+y)=f(x)f(y)　　　　　　　　　　　　 B.f(x-y)=

C.f(nx)=［f(x)］ⁿ D.f［(xy)ⁿ］=［f(x)］ⁿ［f(y)］ⁿ(n∈N^*)

答案：D

解析：易知A、B、C都正确.

对于D,f［(xy)ⁿ］=a^(xy)n,而［f(x)］ⁿ·［f(y)］ⁿ=(a^x)ⁿ·(a^y)ⁿ=a^nx+ny,一般情况下D不成立.