10.函数y=log_a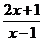的图象恒过定点P,则P点坐标为______________.

答案：(-2,0)

解析：对一切a∈(0,1)∪(1,+∞),

当x=-2时,log_a=0.

∴P点坐标为(-2,0).

9.设y=lg(x²-2x-3)的定义域为M,不等式|x-1|≥a的解集为N,且MN,则a的值为(　　 )

A.a=2　　　　　　　　 B.a≥2　　　　　 C.0≤a≤2　　　　　 D.a≤2

答案：D

解析：x²-2x-3>0x<-1或x>3.

∴M=(-∞,-1)∪(3,+∞).

|x-1|≥ax≤1-a或x≥1+a.

∴N=(-∞,1-a)]∪［1+a,+∞］).

∵MN,

∴a≤2.

或用排除法.

令a=-1,则N=R,由MN,排除A、B、C.

8.函数y=a^x与y=-log_ax(a>0且a≠1)在同一坐标系中的图象只可能是(　　 )

答案：A

解析：y=-log_ax=x.显然两函数的底数一个比1大,另一个在0到1之间,根据指数函数和对数函数的图象特征可以判定.

7.已知log_a(2x²-3x+1)<log_a(x²+2x-3)(0<a<1),求x的取值范围.

解：∵log_a(2x²-3x+1)<log_a(x²+2x-3),

∵0<a<1,

∴2x²-3x+1>x²+2x-3,即x²-5x+4>0.

∴x>4或x<1.

又∵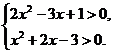

∴

∴x>1或x<-3.

综上可知,当0<a<1时,x的取值集合为{x|x<-3或x>4}.

能力提升　 踮起脚,抓得住!

6.已知0<a<1,0<b<1,<1,则x的取值范围是________________.

答案：3<x<4

解析：∵0<a<1,<1=a⁰,

∴log_b(x-3)>0.

又0<b<1,故0<x-3<1,即3<x<4.

5.函数y=log₂(x-1)的反函数f^-1(x)=____________,反函数的定义域是____________,值域是___________.

答案：2^x+1　 R　 (1,+∞)

解析：∵y=log₂(x-1),

∴x-1=2^y,即x=2^y+1.

∴f^-1(x)=2^x+1.

原函数的定义域(1,+∞)是f^-1(x)的值域,

原函数的值域为R是f^-1(x)的定义域.

4.若f(x)的定义域为［0,1］,则F(x)=f［(3-x)］的定义域是(　　 )

A.［0,1)　　　　　　　 B.［2,)　　　　　　 C.［0,)　　　　 D.(-∞,3)

答案：B

解析：∵F(x)=f［(3-x)］，

∴定义域为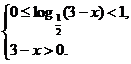

∴

∴

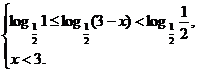
∴2≤x<.

3.已知函数y=f(2^x)的定义域为［-1,1］,则函数y=f(log₂x)的定义域为(　　 )

A.［-1,1］　　　　　　　 B.［,2］　　　　　　　 C.［1,2］　　　　　 D.［,4］

答案：D

解析：∵x∈［-1,1］,∴2^x∈［,2］.

∴log₂x∈［,2］x∈［,4］.

2.函数f(x)=lg(x²-3x+2)的定义域为F,函数g(x)=lg(x-1)+lg(x-2)的定义域为G,则F与G的关系为(　　 )

A.F∩G=　　　　　　 B.F=G　　　　　　　　　 C.FG　　　　　　 D.FG

答案：D

解析：F={x|x²-3x+2>0},G={x|x-1>0且x-2>0}，

∴F={x|x>2或x<1},G={x|x>2}.

GF,即FG.

1.函数y=log₂x+3(x≥1)的值域是(　　 )

A.［2,+∞］)　　　　　　 B.(3,+∞)]　　　　　　　 C.［3,+∞］)　　　　 D.R

答案：C

解析：∵log₂x≥0(x≥1),

∴y=log₂x+3≥3.