
题目列表(包括答案和解析)
14.设A、B是两个非空集合,定义集合A*B={x|x∈A且x B},依以上规定,集合A*(A*B)等于( )
B},依以上规定,集合A*(A*B)等于( )
A.A∩B B.A∪B C.A D.B
答案:A
解析:依题可由韦恩图知A*B表示为

13.设A={x∈R|x2+4x-5=0},B={x∈R|x2+2ax-2a2+3=0,a∈R},
(1)若A∩B=B,求实数a的范围;
(2)若A∩B=A,求实数a的值.
解:(1)由已知得A={-5,1},∵A∩B=B,∴B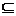 A.则B可能有
A.则B可能有 ,{-5},{1},{-5,1}四种情况.
,{-5},{1},{-5,1}四种情况.
①当B= 时,方程x2+2ax-2a2+3=0无实数解,
时,方程x2+2ax-2a2+3=0无实数解,
∴Δ=4a2-4(-2a2+3)=12(a2-1)<0,即-1<a<1.
②当B={-5}时,Δ=0且(-5)2+2a(-5)-2a2+3=0,a无解,即B≠{-5}.
③当B={1}时,Δ=0且12+2a-2a2+3=0,解得a=-1.
④当B={-5,1}时,由根与系数的关系有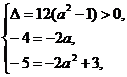 解得a=2,
解得a=2,
综上可得-1≤a<1或a=2.
(2)∵A∩B=A,∴A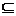 B,
B,
即{-5,1}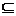 B.∴B={-5,1}.
B.∴B={-5,1}.
由(1)知a=2,即当A∩B=A时,a=2.
拓展应用 跳一跳,够得着!
12.设M={x|x2+mx+n=0,m2-4n>0},A={1,3,5,7,9},B={1,4,7,10}且M∩A= ,M∩B=M,试求m、n的值.
,M∩B=M,试求m、n的值.
解:∵M∩A= ,
,
∴1,3,5,7,9 M.
M.
又∵m2-4n>0,即Δ>0,
∴M中含有两个不同的元素.
而M∩B=M,∴M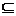 B.
B.
又1,7 M,∴M={4,10}.
M,∴M={4,10}.
由韦达定理得m=-(4+10)=-14,n=4×10=40.
11.设全集为R, A={x|x<-3或x≥4},B={x|x>a},且A∩B=
A={x|x<-3或x≥4},B={x|x>a},且A∩B= ,则实数a的取值范围为________.
,则实数a的取值范围为________.
答案:a≥4
解析:由 A={x|x<-3或x≥4}可知A={x|-3≤x<4},A∩B=
A={x|x<-3或x≥4}可知A={x|-3≤x<4},A∩B= ,由数轴知点P(a)必在A点的右侧时才有A∩B=
,由数轴知点P(a)必在A点的右侧时才有A∩B= ,那么a≥4.
,那么a≥4.

10.集合A含有10个元素,集合B含有8个元素,集合A∩B含有3个元素,那么集合A∪B?有_____________个元素.
答案:15
解析:card(A∪B)=card(A)+card(B)-card(A∩B)=10+8-3=15.
9.若A={x|x=a2+1,a∈N*},B={y|y=b2-4b+5,b∈N*},则结论正确的是( )
A.A、B相等 B.B是A的真子集
C.A是B的真子集 D.以上结论均不正确
答案:C
解析:∵a∈N*,
∴x=a2+1≥2且x∈N.
又∵b∈N*,
∴y=b2-4b+5=(b-2)2+1≥1且y∈N.x、y都是形如n2+1(n∈N)的自然数,但是1∈B而1 A.故A
A.故A B.
B.
8.设A={x|2x2-px+q=0},B={x|6x2+(p+2)x+5+q=0},若A∩B={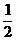 },则A∪B等于( )
},则A∪B等于( )
A.{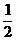 ,-4,
,-4,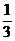 }
B.{
}
B.{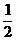 ,-4}
C.{
,-4}
C.{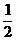 ,
,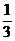 }
D.{
}
D.{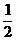 }
}
答案:A
解析:由A∩B={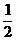 }可知两方程有
}可知两方程有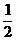 这一根,故有
这一根,故有
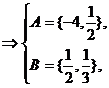 故A∪B={
故A∪B={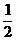 ,
, ,-4}.
,-4}.
7.已知A={x|a≤x≤a+3},B={x|x>5或x<-1}.
(1)若A∩B= ,求a的取值范围;
,求a的取值范围;
(2)若A∪B=B,求a的取值范围.
解:已知A={x|a≤x≤a+3},B={x|x>5或x<-1}.
(1)∵A∩B= ,∴
,∴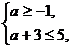 解得-1≤a≤2.
解得-1≤a≤2.
∴所求的a的取值范围为-1≤a≤2.
(2)∵A∪B=B,∴A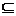 B,
B,
即a>5或a+3<-1.?
解得a>5或a<-4.
∴所求的a的取值范围为a>5或a<-4.
能力提升 踮起脚,抓得住!
6.已知集合A={x|-4≤x<2},B={x|-1<x≤3},C={x|x≤0或x≥ },那么(A∪B)∩C=__________.
},那么(A∪B)∩C=__________.
答案:{x|-4≤x≤0或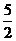 ≤x≤3}
≤x≤3}
解析:画出数轴易得结果.
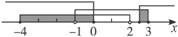
5.已知集合A={y|y=2x+1,x为正实数},集合B={y|y=-x2+9,x∈R},则A∩B=_______________.
答案:{y|1<y≤9=
解析:A的集合也表示为y>1,B的集合表示为y=-(x-3)2+9≤9,∴A∩B={1<x≤9}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com