8.下面结论中,不正确的是(　　 )

A.若0<a<1,0<m<n<1,则一定有log_am>log_an>0

B.函数y=3^x与y=log₃x的图象关于y=x对称

C.函数y=log_ax²与y=2log_ax表示同一函数

D.若a∈(0,1),则y=log_ax与y=a^x在定义域内均为减函数

答案：C

解析：∵y=log_ax²=2log_a|x|=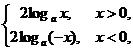

∴与y=2log_ax不表示同一函数.

注意:此题也可以从定义域或者图象等方面考虑两函数是否为同一函数.

7.已知函数f(x)=log_a(a^x-1)(a>1).

(1)求f(x)的定义域;

(2)当x为何值时,函数值大于1;

(3)讨论f(x)的单调性;

(4)解方程f(2x)=f^-1(x).

解：(1)∵a>1,由a^x-1>0,得x>0.

∴f(x)的定义域为(0,+∞).

(2)由log_a(a^x-1)>1,

故当a>1时,x>log_a(a+1),

即当x>log_a(a+1)时,f(x)>1.

(3)当a>1时,f(x)在定义域(0,+∞)上单调递增.

(4)由y=log_a(a^x-1)(a>1)得其反函数为f^-1(x)=log_a(a^x+1).

∴log_a(a^x+1)=log_a(a^2x-1).

∵对数函数在整个定义域上是单调的,

∴有a^x+1=a^2x-1.　 ∴(a^x-2)(a^x+1)=0.

∴a^x=2,a^x=-1(舍去).

∴x=log_a2.

能力提升　 踮起脚,抓得住!

6.设函数f(x)=则满足f(x)=的x值为_________________.

答案：3

解析：当x≤1时,2^-x=()^x≥.

当x>1时,log₈₁x>0,

所以log₈₁x=,x==3.

5.函数y=log_ax的图象向左平移一个单位,再向上平移一个单位后所得图象过点(2,2),则a=___________.

答案：3

解析：依题意知y=log_a(x+1)+1过点(2,2),

∴2=log_a3+1,

即log_a3=1.∴a=3.

4.不等式log_a(x²-2x+3)≤-1在x∈R上恒成立,则a的取值范围是(　　 )

A.［2,+∞)　　　　 　　　　　　　B.(1,2]

C.［,1)　　　　　　　　　　　　 D.(0,)

答案：C

解析：x²-2x+3=(x-1)²+2>2.

又log_a(x²-2x+3)≤-1,

∴0<a<1且≤x²-2x+3对x∈R恒?成立.?

∴≤2≤a<1.

3.已知f(x⁵)=lgx,则f(2)等于(　　 )

A.lg2　　　　　 B.lg32　　　　　　 C.lg　　　　　　　 D.lg2

答案：D

解析：令t=x⁵,则x=,由f(x⁵)=lgx,

有f(t)=lg=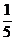lgt,

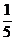∴f(2)=lg2.

2.设函数f(x)=log_ax(a>0,a≠1)满足f(9)=2,则f^-1(log₉2)的值是(　　 )

A.log₃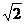　　　　　　　　　　　　 　B.

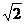C.　　　　　　　　　　　　　　 D.2

答案：C

解析：f(9)=2log_a9=2,a=3.

令log_ax=log₉²,则x=.

1.已知f(x)=(2x+1)在(-,0)内恒有f(x)>0,则a的取值范围是(　　 )

A.a>1　　　　　 B.0<a<1　　　　　　 C.a<-1或a>1　　　　　 D.-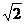<a<-1或1<a<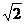

答案：D

解析：∵-<x<0,∴0<2x+1<1.

要使x∈(-,0)时,f(x)>0,则0<a²-1<1,

即1<a²<2,

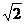∴-<a<-1或1<a<.

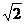16.已知A={x|x²+(p+2)x+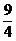p=0,x∈R, p∈R}.

(1)若A∩{正实数}=,求p的取值范围;

(2)若A∩{正实数}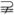,求p的取值范围.

解：Δ=(p+2)²-4×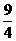p=(p-1)(p-4).

(1)∵A∩{正实数}=,

∴方程x²+(p+2)x+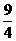p=0无实数解或有非正实数解,于是Δ<0,　　　　　　　　　　　　 ①

或　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

解①得1<p<4;

解②得0≤p≤1或p≥4.

综合①②知p≥0.

(2)方法一:由A∩{正实根},可知A集合中元素可能情况如下:

①两正根;②一正根,一负根;③一零根,一正根;等价于

①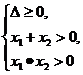或②x₁x₂<0或③

由①②③知p<0.

方法二:对于问题(2)可转化为在Δ≥0前提下A∩{正实数}与A∩{正实数}=是对立的,即在Δ≥0,即p≥4或p≤1情况下,{p|p≥0}的补集为{p|p<0}.

15.满足A∪B={a₁,a₂}的集合A、B共有____________组.

答案：9

解析：(1)A=时,B={a₁,a₂},(2)A={a₁},B={a₂},{a₁,a₂},(3)A={a₂}时,B={a₁},{a₁,a₂},

(4)A={a₁,a₂}时,B=,{a₁},{a₂},{a₁,a₂},故一共有9组.