
题目列表(包括答案和解析)
6.若0<a<1,则不等式(x-a)(x- )>0的解集是___________________.
)>0的解集是___________________.
答案:{x|x> 或x<a}
或x<a}
解析:∵0<a<1,∴ >1.∴x>
>1.∴x> 或x<a.
或x<a.
5.不等式(x-2)(x2-5x+6)≥0的解集为_________________.
答案:{x|x≥3或x=2}
解析:原不等式等价于(x-2)2(x-3)≥0.
4.有以下命题:(1)如果x1、x2是方程ax2+bx+c=0的两个实根,且x1<x2,那么不等式ax2+bx+c<0的解集为{x|x1<x<x2};(2)当Δ=b2-4ac<0时,二次不等式ax2+bx+c>0的解集为 ;(3)
;(3) ≤0与(x-a)(x-b)≤0的解集相同;(4)
≤0与(x-a)(x-b)≤0的解集相同;(4)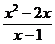 <3与x2-2x<3(x-1)的解集相同.其中正确的命题有( )
<3与x2-2x<3(x-1)的解集相同.其中正确的命题有( )
A.3个 B.2个 C.1个 D.0个
答案:D
解析:(1)(2)中要考虑a的符号,(3)要注意分母不为0,(4)要注意分母符号.
3.下列不等式解集为 的是( )
的是( )
A.x2+2x-1≤0 B.x2+4x+4≤0
C.4-4x-x2<0 D.2-3x+2x2≤0
答案:D
解析:A.{x|-1- ≤x≤-1+
≤x≤-1+ },B.{-2},C.{x|x>2
},B.{-2},C.{x|x>2 -2或x<-2
-2或x<-2 -2}.
-2}.
2.与不等式 >0有相同解集的是( )
>0有相同解集的是( )
A.x2-1<0 B.x2-1>0
C. D.
D. >0
>0
答案:A
解析:原不等式等价于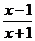 <0,又等价于?(x+1)?(x-1)<0.
<0,又等价于?(x+1)?(x-1)<0.
1.不等式(x+2)(3-x)>0的解集为( )
A.{x|x>3或x<-2} B.{x|-3<x<2}
C.{x|x>2或x<-3} D.{x|-2<x<3}
答案:D
解析:注意将(3-x)中x的符号变正后,不等号反向.
16.设不等式|x+1|-|x-2|>k的解集为R,求实数k的取值范围.
解法一:根据绝对值的几何意义,|x+1|可以看作数轴上点P(x)到点A(-1)的距离|PA|,|x-2|可以看作是数轴上点P(x)到点B(2)的距离|PB|,则|x+1|-|x-2|=|PA|-|PB|.如图所示:

当点P在线段AB上时,-3≤|PA|-|PB|≤3,
当P在A点左侧时,|PA|-|PB|=-3,
当P在B点右侧时,|PA|-|PB|=3,
则不等式-3≤|x+1|-|x-2|≤3恒成立.
故使原不等式的解集为R的实数k的取值范围是k<-3.
解法二:令y=|x+1|-|x-2|
=
在直角坐标系中,作出函数图象如图.

要使不等式|x+1|-|x-2|>k对一切实数成立,则函数图象全部都落在直线y=k的上方,则k的取值范围为k<-3.
15.已知关于x的不等式|x+2|+|x-3|<a的解集非空,则实数a的取值范围是________________.
答案:a>5
解析:∵|x+2|+|x-3|≥5恒成立,
∴当a≤5时,|x+2|+|x-3|<a解集为 .
.
故要使|x+2|+|x-3|<a解集非空,则应有a>5.
14.已知a∈R,则(1-|a|)(1+a)>0的解集为( )
A.|a|<1 B.a<1 C.|a|>1 D.a<1且a≠-1
答案:D
解析:(1)a≥0时,(1-|a|)(1+a)=(1-a)(1+a)>0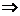 0≤a<1;
0≤a<1;
(2)a<0时,(1+a)(1+a)=(1+a)2>0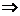 a<0,且a≠-1.
a<0,且a≠-1.
综合知a<1,且a≠-1.
13.关于实数x的不等式|x- |≤
|≤ 与|x-a-1|≤a的解集依次记为A与B,求使A
与|x-a-1|≤a的解集依次记为A与B,求使A B的a的取值范围.
B的a的取值范围.
解:由|x- |≤
|≤ ,
,
得- ≤x-
≤x- ≤
≤ ,
,
所以2a≤x≤a2+1.
由|x-a-1|≤a,得-a≤x-a-1≤a,则1≤x≤2a+1,要使A B,就必须
B,就必须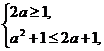 即
即 故a的取值范围为
故a的取值范围为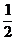 ≤a≤2.
≤a≤2.
拓展应用 跳一跳,够得着!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com