12.已知函数f(x)=(a、b为常数,a≠0)满足f(2)=1,f(x)=x有唯一解,求函数f(x)的解析式和f［f(-3)］的值.

解：∵f(2)=1,∴1=,即2a+b=2.　　　　　　　　　　　　　　　　　　　　　 ①

又∵f(x)=x有唯一解,即=x有唯一解,∴x·=0.

解之,得x₁=0,x₂=,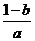

∵有唯一的解,∴x₁=x₂=0,得b=1.　　　　　　　　　　　　　　　　　　 　　　　　　　②

由①②得a=,b=1.

∴f(x)=.

故f［f(-3)］=f(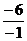)=f(6)= .

11.下列对应:

(1)A=R⁺,B=R,对应法则是“求平方根”.

(2)A={x|-3≤x≤3},B={y|0≤y≤1},对应法则是“平方除以9”.

(3)A={x|x∈N^*},B={-1,1},对应法则f:x→y=(-1)^x(x∈A,y∈B).

(4)A={平面α内的圆},B={平面α内的矩形},对应法则是“作圆内接矩形”.

(5)A=R,B=R⁺,f:x→y=x²-1.

其中,是A到B的映射有_________________.(将是映射的序号全部填上)

答案：(2)(3)

解析：映射是一类特殊的对应,可一对一或多对一的对应,但不能是一对多的对应.

10.设A到B的映射f₁:x→2x+1,B到C的映射f₂:y→y²-1,则A到C的映射f₃是____________.

答案：z→4z²+4z

解析：x→2x+1,(2x+1)²-1=4x²+4x,即z→4z²+4z.

9.确定函数y=x²+1的对应关系是(　　 )

A.f:R→R　　　　　　　　　　　　　　　　 B.f:(0,+∞)→(0,+∞)

C.f:R→(0,+∞)　　　　　　　　　　　　　　 D.f:R→［1,+∞)

答案：D

解析：函数y=x²+1的定义域是R,对任意的x∈R,有y=x²+1≥1,即y∈［1,+∞).

8.下面三个对应(Z为整数集);(1)Z中的元素x与2x对应;(2)Z中的元素x与对应;(3)Z中的元素x与x²-1对应,其中Z到Z的映射有(　　 )

A.0个　　 　　　　　　　B.1个　　　　　　 C.2个　　　　　　　 D.3个

答案：C

解析：根据A中元素任意性,B中元素唯一性知(1)(3)对.

7.在下列各个条件下求f(x):

(1)f(2x+1)=x²-3x+1;

(2)f()=;

(3)f(x+)=x²+.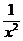

解：(1)设2x+1=t,则x=.

∴f(t)=f(2x+1)=x²-3x+1=()²-3·+1=-2t+.

∴f(x)=-2x+.

(2)设t=≠0,则x=.

∴f(t)=.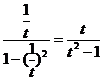

∴f(x)=(x∈R且x≠0,x≠±1).

(3)∵f(x+)=x²+=(x+)²-2,

∴f(x)=x²-2,x∈(-∞,-2)∪［2,+∞］.

能力提升　 踮起脚,抓得住!

6.设函数f(x)=若f(x)=3,则x=_______________.

答案：

解析：分别讨论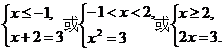

5.如果映射f:A→B的象的集合是Y,原象的集合是X,那么X与A的关系是_______________;Y与B的关系是__________________.

答案：X=A　 Y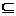B

解析：由函数定义易知.

4.设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示集合M到集合N的函数关系的有(　　 )

A.0个　　　　　　　　　 B.1个　　　　　　　 C.2个　　　　　　　 D.3个

答案：C

解析：由图象及函数的定义域与值域可知②③正确.

3.下列各组中的函数图象相同的是(　　 )

A.f(x)=1,g(x)=x⁰ B.f(x)=1,g(x)=

C.f(x)=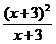,g(x)=(x+3)(x+3)⁰ D.f(x)=|x|,g(x)=

答案：C

解析：考查定义域与对应法则.