
题目列表(包括答案和解析)
16.已知函数f(x)的值域是[ ],求函数y=f(x)+
],求函数y=f(x)+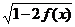 的值域.
的值域.
解:设t=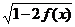 ,则f(x)=
,则f(x)=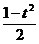 ,
,
∵f(x)的值域为[ ,
, ],
],
∴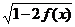 ∈[
∈[ ,
,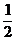 ],即t∈[
],即t∈[ ,
,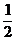 ].
].
又∵y=f(x)+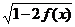 ,
,
∴y=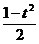 +t=-
+t=-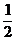 t2+t+
t2+t+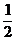 (
( ≤t≤
≤t≤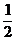 ).
).
∴ ≤y≤
≤y≤ .
.
∴函数y=f(x)+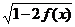 的值域为[
的值域为[ ].
].
15.若函数y= 的定义域是R,则实数a的取值范围是_________________.
的定义域是R,则实数a的取值范围是_________________.
答案:(0,2)
解析:因为a≠0,所以对一切实数x,不等式ax2-ax+ ≥0恒成立,
≥0恒成立,
故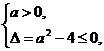 解得0<a≤2.
解得0<a≤2.
故a的取值范围是(0,2].
14.函数y=x2-4x+1,当0≤x≤3时,则函数的值域是( )
A.(-∞,+∞) B.[-3,+∞) C.(-3,+∞) D.[-3,1]
答案:D
解析:因为y=x2-4x+1=(x-2)2-3,当0≤x≤3时,(x-2)2-3∈[-3,1],故选D.
13.(1)求函数f(x)= (a∈R)的定义域;
(a∈R)的定义域;
(2)已知f(x)=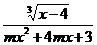 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
解:(1)由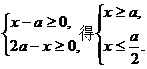
当a>0时,∵a> ,∴x为空集;
,∴x为空集;
当a≤0时,∵a≤ ,∴a≤x≤
,∴a≤x≤ .
.
∴a≤0时,f(x)的定义域为{x|a≤x≤ }.
}.
(2)由题意知mx2+4mx+3≠0的解集为R.
当m=0时,3≠0,解集为R,符合条件;当m≠0时,要使mx2+4mx+3≠0的解集为R,就是使函数g(x)=mx2+4mx+3的图象与x轴没有公共点,∴Δ<0,即(4m)2-4·m·3<0,解得0<m< .综上,知0≤m<
.综上,知0≤m< 为所求.
为所求.
拓展应用 跳一跳,够得着!
12.设函数f(x)=- 的定义域为A,函数g(x)=
的定义域为A,函数g(x)=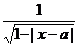 的定义域为B,求当A∩B=
的定义域为B,求当A∩B= 时a的取值范围.
时a的取值范围.
解:由-x2+2x+8≥0,得x2-2x-8≤0 A=[-2,4],
A=[-2,4],
由1-|x-a|>0,得|x-a|<1-1+a<x<1+a,即B=(-1+a,1+a).
∵A∩B= ,
,
∴-1+a≥4或1+a≤-2.
解得a∈(-∞,-3)∪[5,+∞].
11.函数f(x)的定义域为[0,2],则函数y=f(x+2)的定义域为________________.
答案:[-2,0]
解析:∵f(x)的定义域为[0,2],
∴f(x+2)的x+2应满足0≤x+2≤2,
即-2≤x≤0.
∴y=f(x+2)的定义域为[-2,0].
10.函数y= 的值域是__________________.
的值域是__________________.
答案:{y|y≠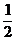 }
}
解析:函数y= 的值域为{y|y≠0},
的值域为{y|y≠0},
而y=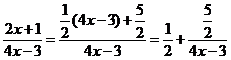 ≠
≠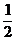 ,一般地,y=
,一般地,y=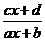 的值域为{y|y≠
的值域为{y|y≠ ,y∈R}.
,y∈R}.
9.函数y=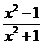 的值域是( )
的值域是( )
A.[-1,1] B.[-1,1)
C.(-1,1) D.(-1,1)
答案:B
解析:反解得x2= ≥0,
≥0,
∴-1≤y<1.
8.已知函数f(x)=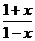 的定义域为A,函数y=f[f(x)]的定义域为B,则( )
的定义域为A,函数y=f[f(x)]的定义域为B,则( )
A.A∪B=B
B.A B
B
C.A=B D.A∩B=B
答案:D
解析:函数y=f[f(x)]的定义域由 确定,故B
确定,故B A,则A∩B=B.
A,则A∩B=B.
7.求下列函数的值域.
(1)y=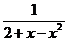 ;
;
(2)y= (a>b>0,-1≤x≤1).
(a>b>0,-1≤x≤1).
解:(1)∵-x2+x+2=-(x-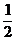 )2+
)2+ ,而-x2+x+2=-(x-
,而-x2+x+2=-(x-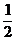 )2+
)2+ ≤
≤ ,此时有三种情况:若-(x-
,此时有三种情况:若-(x-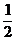 )2+
)2+ <0,则y=
<0,则y=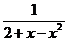 <0;
<0;
若-(x-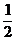 )2+
)2+ =0,则y无意义;若-(x-
=0,则y无意义;若-(x-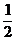 )2+
)2+ >0,我们可看到-(x-
>0,我们可看到-(x-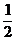 )2+
)2+ ≤
≤ ,则有y=
,则有y=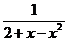 ≥
≥ .
.
∴函数y=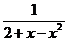 的值域是(-∞,0)∪[
的值域是(-∞,0)∪[ ,+∞).
,+∞).
(2)y= (a>b>0,-1≤x≤1)等价于y=-
(a>b>0,-1≤x≤1)等价于y=- .
.
∵-1≤x≤1,a>b>0,
∴-b≤-bx≤b.
0<a-b≤a-bx≤a+b, ≤
≤ ≤
≤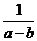 ,
,
∴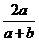 ≤
≤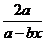 ≤
≤ ,
,
-1+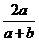 ≤
≤ ≤
≤ -1,
-1,
 ≤y≤
≤y≤ .
.
∴函数y= 的值域是[
的值域是[ ].
].
能力提升 踮起脚,抓得住!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com