8.函数y=-|x-1|(x+5)的单调增区间为(　　 )

A.(-∞,-2]　　　　　　　 B.［-2,+∞)　　　　　　 C.［-2,1)　　　　　　 D.［1,+∞)

答案：C

解析：y=-|x-1|(x+5)=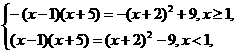由图形易知选C.

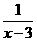7.已知f(x)是定义在(0,+∞)上的增函数,且f()=f(x)-f(y),f(2)=1,解不等式f(x)-f()≤2.

解：2=f(2)+f(2),而f()=f(x)-f(y)可以变形为f(y)+f()=f(x).

令y=2,=2,即x=2y=4,

则有f(2)+f(2)=f(4),∴2=f(4).

∴f(x)-f(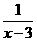)≤2可以变形为f［x(x-3)］≤f(4).

又∵f(x)是定义在(0,+∞)上的增函数,

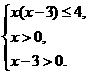∴解得3<x≤4.

∴原不等式的解集为{x|3<x≤4}.

能力提升　 踮起脚,抓得住!

6.已知f(x)在R上满足f(-x)+f(x)=0,且在［0,+∞］上为增函数,若f(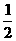)=1,则-1<f(2x+1)≤0的解集为__________________.

答案：(-,-]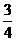

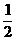解析：由f(-x)+f(x)=0f(0)=0,

f(-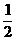)=-1,故由-1<f(2x+1)≤0f(-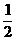)<f(2x+1)≤f(0),可证f(x)在R上为增函数,故-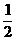<2x+1≤0-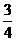<x≤-.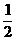

5.若函数f(x)=ax²+2x+5在(2,+∞)上是单调递减的,则a的取值范围是______________.

答案：a≤-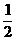

解析：若a=0,则f(x)=2x+5,与已知矛盾,∴a≠0.

这时,f(x)=ax²+2x+5=a(x+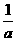)²+5-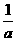,对称轴为x=-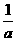,由题设知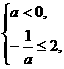,解得a≤-.

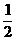4.已知函数f(x)=x²-6x+7的图象如图所示,下列四个命题中正确的命题个数为(　 　)

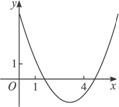
(1)函数在(-∞,1］上单调递减　

(2)函数的单调递减区间为(-∞,1］　 (3)函数在［3,4］上单调递增　 (4)函数的单调递增区间为［3,4］

A.1　　　　　　　　 B.2　　　　　　　 C.3　　　　　　　 D.4

答案：B

解析：由图形知(1)(3)正确;函数的单调递增区间为［3,+∞),递减区间为(-∞,3],故(2)(3)错误.

3.函数f(x)在定义域上单调递减，且过点(-3,2)和(1,-2),则使|f(x)|<2的自变量x的取值范围是(　　 )

A.(-3,+∞)　　　　　　 B.(-3,1)　　　　　 C.(-∞,1)　　　　　 D.(-∞,+∞)

答案：B

解析：|f(x)|<2-2<f(x)<2f(1)<f(x)<f(-3),又f(x)单调递减,故-3<x<1.

2.设f(x)为定义在A上的减函数,且f(x)>0,则下列函数:(1)y=3-2 004f(x);(2)y=1+;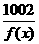

(3)y=f²(x);④y=2 005+f(x).其中为增函数的个数是(　　 )

A.1　　　　　　　　　 B.2　　　　　　 C.3　　　　　　　　 D.4

答案：B

解法一:令f(x)=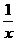(x>0),则(1)y=3-2 004f(x)=3-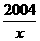;(2)y=1+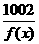=1+1 002x;

(3)y=f²(x)=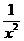;(4)y=2 005+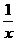在(0,+∞)上为增函数的是(1)(2),故正确命题的个数为2.

解法二:利用单调函数的定义判断.

1.已知函数y=ax²+bx+c(a<0)图象的对称轴为直线x=3,则下列关系式中,不正确的是(　　 )

A.f(6)<f(4)　　　　　　　　　　　　　　 B.f(2)<f()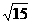

C.f(3+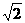)=f(3-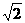)　　　　　　　　　 D.f(0)<f(7)

答案：D

解析：依题意,函数y=ax²+bx+c在(-∞,3)内递增,在［3,+∞］内递减,故f(0)=f(6)>f(7).

16.已知函数f(x)=,x∈［1,+∞).

(1)当a=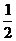时,求函数f(x)的最小值;

(2)若对任意x∈［1,+∞),f(x)>0恒成立,求实数a的取值范围.

解：(1)当a=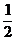时,f(x)=x+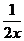+2,设1≤x₁<x₂,

则f(x₂)-f(x₁)=x₂+-(x₁+)=.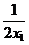

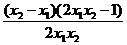因为1≤x₁<x₂,所以x₂-x₁>0,2x₁x₂-1>0,2x₁x₂>0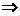f(x₂)-f(x₁)>0,

即f(x)在［1,+∞］上单调递增,f(x)_min=f(1)=1+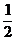+2=.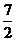

(2)x∈［1,+∞］,f(x)>0恒成立x²+2x+a>0恒成立,即a>-x²-2x恒成立,又y=-x²-2x=

-(x+1)²+1≤-3,所以a>-3.

15.老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质:

甲:对于x∈R,都有f(1+x)=f(1-x);

乙:在(-∞,0］上函数递减;

丙:在(0,+∞)上函数递增;

丁:f(0)不是函数的最小值.

如果其中恰有三人说得正确,请写出一个这样的函数:________________.

答案：f(x)=(x-1)²(不唯一)

解析：f(x)=(x-1)²(答案不唯一,满足其中三个且另一个不满足即可).

f(1+x)=f(1-x)表示对称轴方程为x=1.