
题目列表(包括答案和解析)
6.某校高三年级学生年龄分布在17岁、18岁、19岁的人数分别为500、400、100,现通过分层抽样从上述学生中抽取一个样本容量为 的样本,已知每位学生被抽到的概率都为0.2,则
的样本,已知每位学生被抽到的概率都为0.2,则 ▲ .
▲ .
5.已知 =(2,4),
=(2,4),
 =(-1,-3), 则 |3
=(-1,-3), 则 |3 +2
+2 |= ▲
|= ▲
4.在20瓶饮料中,有两瓶是过了保质期的,从中任取1瓶,恰为过保质期的概率为_ ▲___
3.某城市有学校 所,其中大学
所,其中大学 所,中学
所,中学 所,小学
所,小学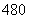 所.现用分层抽样的方法从中抽取一个容量为
所.现用分层抽样的方法从中抽取一个容量为 的样本进行某项调查,则应抽取的中学数为 ▲ .
的样本进行某项调查,则应抽取的中学数为 ▲ .
2.统计某校800名学生的数学期末成绩,得到频率分布直方图如图示,若考试采用100分制,并规定不低于60分为及格,则及格率为 ▲ .


1.已知集合 ,
,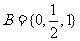 ,若
,若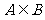 ,则锐角
,则锐角 ▲ .
▲ .
20、已知n条直线:L1:x-y+C1=0、C1
= , L2:x-y+C2=0,L3:x-y+C3=0,
, L2:x-y+C2=0,L3:x-y+C3=0,
……Ln:x-y+Cn=0 .(其中C1< C2 <C3 <……< Cn)这n条平行线中,每相邻两条之间的
距离顺次为2,3,4,……,n.
(1)求Cn ;
(2)求x-y+Cn=0与x轴、y轴围成的图形的面积;
(3)求x-y+Cn-1=0与x-y+Cn=0及x轴、y轴围成的图形的面积.
部分答案
7[解析]:解:(1)由题意可知:L1到Ln的距离为: =2+3+4+……+n,
=2+3+4+……+n,
∵ >
> ∴
∴ =
= .
.
(2)设直线Ln:x-y+cn=0交x轴于M点,交y轴于N点,则△OMN的面积为:
S△OMN= │OM││ON│=
│OM││ON│=
 =
= .
.
(3)围成的图形是等腰梯形,由(2)知Sn= .则有
.则有
Sn-1=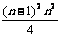 Sn-Sn-1=
Sn-Sn-1=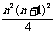 -
- =n3 所以所求面积为n3.
=n3 所以所求面积为n3.
5解法一:(1)把y=2mx-8m-3代入圆C,得
(4m2+1)x2+?2(-16m2+6m-3)x+(64m2-48m-7)=0.
∵Δ=64×(6m2+1)>0,∴l与C总相交.
(2)设交点为A、B,由弦长公式得|AB|= |x1-x2|,
|x1-x2|,
即|AB|=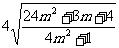 .
.
令 ,得4×(6-t)m2+3m+4-t=0.
,得4×(6-t)m2+3m+4-t=0.
∵m∈R,∴Δ=9-4×4(6-t)(4-t)≥0.
解得 ,t最小值为
,t最小值为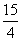 ,此时
,此时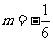 .
.
∴当l被C截得的线段最小值为 ,此时l的方程为x+3y+5=0.
,此时l的方程为x+3y+5=0.
解法二:(1)圆心C(3,-6)到l的距离
 4(d2-1)m2+12m+d2-9=0,(*)
4(d2-1)m2+12m+d2-9=0,(*)
∵m∈R,∴Δ=122-4×4(d2-1)(d2-9)≥0.
解得0≤d≤
 d<R.
d<R.
故不论m为何实数,l与C总相交.
(2)由(1)知d最大为 ,所以弦|AB|最小=2
,所以弦|AB|最小=2 ,把
,把 代入(*)得
代入(*)得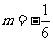 .
.
∴当l被C截得的线段最短时l的方程为x+3y+5=0.
解法三:(1)由直线方程知l过定点M(4,-3),而?(4-3)2+ (-3+6)2=10<25,
∴M在圆内.
∴不论m取何实数,l与C都相交.
(2)由几何知识知当l被C截得线段中点为M时,弦心距最大而弦长最短,此时MC与l垂直.
∴MC斜率为 .
.
∴l斜率为 ,即m
,即m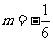 .
.
此时l的方程为x+3y+5=0.
(1)当直线 的斜率存在时,设它的斜率为
的斜率存在时,设它的斜率为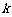 ,
,
则直线 可表示为:
可表示为: , 即
, 即 ,
,
点P到直线 的距离为:
的距离为: ,即
,即 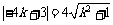 ,
, ,
,
此时直线 的方程为:
的方程为: 即
即  ;
;
(2)当直线 的斜率不存在时,即倾斜角为
的斜率不存在时,即倾斜角为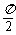 时,也符合题意,
时,也符合题意,
此时直线 的方程为
的方程为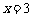 ;
;
综合(1)(2),直线 的方程为:
的方程为: 和
和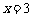 .
.
解:(I)“抽出的3张卡片上最大的数字是4”的事件记为A,由题意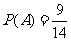
(II)“抽出的3张中有2张卡片上的数字是3”的事件记为B,则 
(III)“抽出的3张卡片上的数字互不相同”的事件记为C,“抽出的3张卡片上有两个数字相同”的事件记为D,由题意,C与D是对立事件,因为  所以
所以 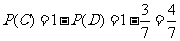 .
.
[解析] (Ⅰ)由题设得 ,即
,即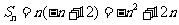 .
.
(Ⅱ)当 时,
时,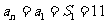 ;
;
当 时,
时,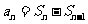 =
= =
= ;
;
由于此时-2×1+13=11= ,从而数列
,从而数列 的通项公式是
的通项公式是 .
.
(Ⅲ)由(Ⅱ)知, ,数列
,数列 从第7项起均为负数.设数列
从第7项起均为负数.设数列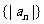 的前n项的和为
的前n项的和为 .
.
当 时,
时,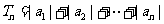 =
= =
= ;
;
当 时,
时,

=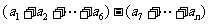
=
= =
= .
.
所以数列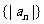 的前n项的和为
的前n项的和为 .
.
19、已知直线l:2mx-y-8m-3=0和圆C:(x-3)2+(y+6)2=25.
(1)证明不论m取什么实数,直线l与圆C总相交;
(2)求直线l被圆C截得的线段最短时的直线l方程.
18、设数列 的前n项和为
的前n项和为 ,点
,点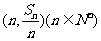 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.
(Ⅰ)写出 关于n的函数表达式;
关于n的函数表达式;
(Ⅱ)求数列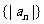 的前n项的和
的前n项的和
17、盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,每张卡片被抽出的可能性都相等,求:(Ⅰ)抽出的3张卡片上最大的数字是4的概率;(Ⅱ)抽出的3张中有2张卡片上的数字是3的概念;(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com