
题目列表(包括答案和解析)
4.数据a1,a2,a3,…,an的方差为σ2,则数据2a1+1,2a2+1,2a3+1,…,2an+1的方差为( )
A. B.σ2
B.σ2
C.2σ2 D.4σ2
3.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y+2)2=100 B.(x-1)2+(y-2)2=100
C.(x-1)2+(y-2)2=25 D.(x+1)2+(y+2)2=25
20、(本题满分16分)
已知两个非零向量 ,
, ,
, 。
。
(Ⅰ)当 =2,
=2, 时,向量
时,向量 与
与 共线,求x的值;
共线,求x的值;
(Ⅱ)若函数 的图象与直线
的图象与直线 的任意两个相邻交点间的距离都是
的任意两个相邻交点间的距离都是 ;
;
① 当 ,
,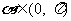 时,求
时,求 的值;
的值;
② 令 ,
,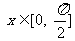 ,试求函数g (x)的值域。
,试求函数g (x)的值域。
19、(本题满分16分)
已知函数 。
。
(1)求函数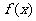 的周期;
的周期;
(2)若函数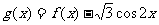 ,试求函数
,试求函数 的单调递增区间;
的单调递增区间;
(3)若f 2 (x) – cos2x ≥m 2 – m – 3恒成立,试求实数m的取值范围。
18、(本题满分15分)
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3 s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间。
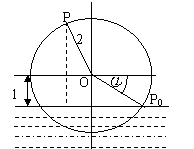 (1)试建立适当的坐标系,将点P距离水面的高度h(m)表示为时间t(s)的函数;
(1)试建立适当的坐标系,将点P距离水面的高度h(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约要多长时间?
(3)记f(t)=h,求证:不论t为何值,
f (t) + f (t + 1) + f (t + 2)是定值。
17、(本题满分15分)
已知向量 函数f (x) =
函数f (x) =  的图象经过点(
的图象经过点( ,2)。
,2)。
(1)求实数m的值。
(2)求函数f (x)的最小值及取得最小值时的x的集合;
(3)函数y=
f (x)的图象可以由函数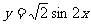 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
16、(本题满分14分)
(1)求值: ;
;
(2)已知向量 ,
, ,其中
,其中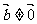 ,若
,若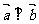 ,试求实数m的取值范围。
,试求实数m的取值范围。
15、(本题满分14分)
已知| |=1,|
|=1,| |=
|=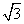 ,
, +
+ =(
=(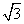 ,1),
,1),
(1)求| –
– |的值;
|的值;
(2)求向量 +
+ 与与向量
与与向量 –
– 的夹角
的夹角
14、如图,当点P、Q三等份线段AB时,有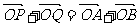 ;如果点A1,A2,……,
;如果点A1,A2,……,
 An – 1是AB的n(n≥3)等份点,则
An – 1是AB的n(n≥3)等份点,则 =
(
=
( )。
)。
二:解答题(共六大题,计90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com