
题目列表(包括答案和解析)
9.下列命题中正确的是( )
A.{x|x=2n-1,n∈R且1≤n≤5}是一个有限集
B.方程x2-2x+1=0的解集是{1,1}
C.已知A={a,b},B={b,a},则A与B不相同
D.如果A={x,y}表示一个数集,则x≠y
答案:D
解析:由1≤n≤5得1≤2n-1≤9,即1≤x≤9,从而知该集合中的元素是1到9之间的任何实数,是一个无限集,即排除A项;方程x2-2x+1=0有两个相等的实根,x1=x2=1,但{1,1}不符合集合元素的互异性.即排除B项;因为任何集合的元素具有无序性,从而A与B相同,即排除C项;因为任何集合的元素具有互异性,则x≠y正确.
8.设a、b、c为非零实数,则M= 的所有值组成的集合为( )
的所有值组成的集合为( )
A.{4} B.{0} C.{-4} D.{4,0,-4}
答案:D
解析:若a、b、c全正,则M=4;若两正一负,则M=0;若两负一正,则M=0;若全负,则M=-4.
7.若9∈{1,2,a2},且9 (2,a+6),求实数a的值.
(2,a+6),求实数a的值.
解:∵9∈{1,2,a2},∴a2=9,得a=±3.
又9 {2,a+6},∴a+6≠9.
{2,a+6},∴a+6≠9.
∴a≠3.故a=-3.
能力提升 踮起脚,抓得住!
6.对于集合A={2,4,6},若a∈A,则6-a∈A,那么a的值是_____________.
答案:2或4
解析:若2∈A,则6-2=4∈A;若4∈A,则6-4=2∈A.而若6∈A,则6-6=0 A,不符合题意.
A,不符合题意.
5.若集合A={x|kx2+4x+4=0,x∈R}中只有一个元素,则实数k的值为______________.
答案:0或1
解析:若k=0,则4x+4=0,∴x=-1,A={-1};若k≠0,Δ=0,得k=1,综上,k=0或k=1.
4.已知集合M={1,2,x2},则x满足条件( )
A.x≠1且x≠ B.x≠±1
B.x≠±1
C.x≠± D.x≠±1且x≠±
D.x≠±1且x≠±
答案:D
解析:由元素的互异性可知.
3.集合{1,3,5,7,9}用描述法表示应是( )
A.{x|x是不大于9的非负奇数} B.{x∈N|1≤x≤9}
C.{x∈Z|0≤x≤9} D.{x∈N|x≤9}
答案:A
解析:集合中的元素是小于或等于9的正奇数.
2.下面四个关系式:
(1)0.2∈N;(2)0 N;(3)
N;(3)
 Z;(4)0∈
Z;(4)0∈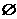 .
.
其中正确的个数是( )
A.3 B.2 C.1 D.0
答案:C
解析:首先认清N即为自然数集,Z即为整数集,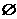 为不含任何元素的空集.因而有0.2
为不含任何元素的空集.因而有0.2 N,0∈N,
N,0∈N, 为有理数、非整数,故
为有理数、非整数,故
 Z是正确的,0
Z是正确的,0
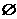 .
.
1.不能形成集合的是( )
A.所有的直角三角形 B.12的正约数
C.我国的大河流 D.全体有理数
答案:C
解析:由元素的确定性可知.
20.正项数列{ }的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当
}的前n项和为Sn,q为非零常数.已知对任意正整数n, m,当 时,
时,
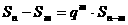 总成立.
总成立.
(1)求证:数列{ }是等比数列;
}是等比数列;
(2)若互不相等的正整数n, m, k成等差数列,比较
 的大小;
的大小;
(3)若正整数n, m, k成等差数列,求证: +
+ ≥
≥ .
.
证明:(1)因为对任意正整数n, m,当n > m时,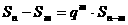 总成立
总成立
所以当 ≥2时:
≥2时: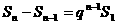 ,即
,即 ,且
,且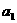 也适合,又
也适合,又 >0,
>0,
故当 ≥2时:
≥2时: (非零常数),即{
(非零常数),即{ }是等比数列
}是等比数列
(2)若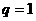 ,则
,则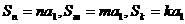
所以
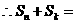

若
 ,则
,则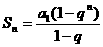 ,
, ,
,
所以

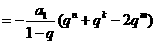
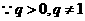
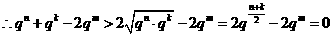
①若
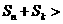
 ②若
②若


(3)若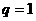 ,则
,则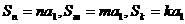 所以
所以
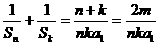 ≥
≥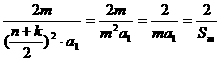
若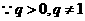 ,则
,则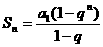 ,
, ,
,
所以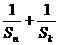 ≥
≥
又因为
≤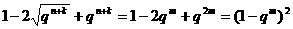 。
。
所以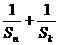 ≥
≥ ≥
≥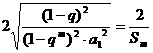 。
。
综上可知:若正整数n, m,
k成等差数列,不等式
 +
+ ≥
≥ 总成立
总成立
(当且仅当 时取“=”)
时取“=”)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com