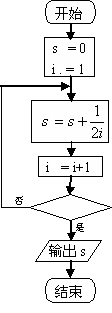
3. 右图给出的是计算的值的一个流程图，其中判断

框内应填入的条件是(　).

A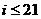．　 　B．　 　　C．　　　 D．

2.线性回归方程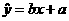表示的直线必经过的一个定点是(　).

A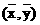．　　　 B．　 　　　C．　　　　 D．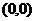

1.下列给出的赋值语句正确的是(　).

A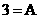．　　　　 B．　　　 C．　　 D．

16.已知集合A={x∈R|ax²-3x+2=0}.

(1)若A=,求实数a的取值范围;

(2)若A是单元素集,求a的值及集合A;

(3)求集合P={a∈R|a使得A≠}.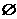

解：(1)若A=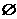,即方程ax²-3x+2=0无解.

若a=0,方程有一根x=,不合题意,则a≠0.

若a≠0,要使方程ax²-3x+2=0无解,则Δ=9-8a<0,即a>.

故使A=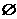的a的取值范围为a>.

(2)当a=0时,由(1)可知,A={},符合题意;

当a≠0时,要使方程有两个相等的实根,则

Δ=9-8a≥0,即a≤.

Δ=9-8a=0,即a=,此时A={}.

综上所述,当a=0时,A={};

当a=时,A={}.

(3)由上知:当a=0时,A={}≠,

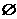当a≠0时,要使方程有实根,则Δ=9-8a≥0,即a≤.

综上所述,P={a∈R|a使得A≠}={a|a≤}.

15.含有三个实数的集合既可表示为{a,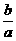,1},又可表示为{a²,a+b,0},则a^{2 004}+b^{2 005}的值为______________.

答案：1

解析：由0∈{a,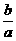,1}得a≠0,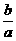≠1,∴b=0,

从而集合变为{a,0,1}={a²,a,0},

进而有a²=1.∴a=1(舍去)或a=-1.

∴a^{2 004}+b^{2 005}=(-1)^{2 004}+0^{2 005}=1.

14.由实数,|x|,-x,x组成的集合,最多含有(　　 )

A.2个元素　　　　　 B.3个元素　　　　 C.4个元素　　　　 D.5个元素

答案：A

解析：=|x|,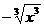=-x,故只考虑|x|、x、-x,若x=0,只有一个元素:|x|=x=-x=0;若x>0,则|x|=x,含有两个元素x、-x;若x<0,则|x|=-x,含有两个元素x、-x.故这5个数组成的集合最多只含有两个元素.

13.已知集合A={a+2,(a+1)²,a²+3a+3},若1∈A,求实数a的值.

解：∵1∈A,∴讨论如下:

(1)若a+2=1,则a=-1.这时有(a+1)²=0,a²+3a+3=(-1)²+3×(-1)+3=1,出现a+2=a²+3a+3,这与集合元素的互异性相矛盾,故a≠-1.

(2)若(a+1)²=1,解得a=0,或a=-2.当a=0时,a+2=2,a²+3a+3=3,这时集合A={1,2,3};当a=-2时,a+2=0,a²+3a+3=1,出现(a+1)²=a²+3a+3,不合题意.

(3)若a²+3a+3=1,则a²+3a+2=0,解得a=-1或a=-2,由(1)知a≠-1.

当a=-2时,a+2=0,(a+1)²=1.这时(a+1)²=a²+3a+3,不合题意.

综上有a=0.

拓展应用　 跳一跳，够得着！

12.已知集合A={x|ax²+2x+1=0,a∈R,x∈R},

(1)若A中只有一个元素,求a的值,并求出这个元素;

(2)若A中只有两个元素,求a的取值范围.

解：(1)①当a=0时,方程2x+1=0只有一个根,x=-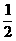;②a≠0时,Δ=4-4a=0,得a=1,这时x₁=x₂=-1,所以a=0或a=1时,A中只有一个元素,分别为-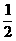或-1.

(2)若A中有两个元素,则方程ax²+2x+1=0,必须且只需有2个不同的根,

∴

∴a的取值范围是{a|a<1且a≠0}.

11.集合A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z},C={x|x=4k+1,k∈Z},若a∈A,c∈C,则a+c与集合B的关系为__________.

答案：(a+c)∈B

解析：因为a∈A,c∈C,故可令a=2m,c=4n+1(m、n∈Z),故有a+c=2m+4n+1=2(m+2n)+1∈B.

10.已知集合P={x|ax+b-x+2=0}为无限集,则a+b=___________.

答案：-1

解析：集合P为无限集即方程有无数多个解,即(a-1)x=-2-b恒成立,此时a=1,b=-2,故a+b=-1.