
题目列表(包括答案和解析)
4.某程序框图所示,若输出的S=57,则判断框内为( )
(A) k>4? (B) k>5? (C) k>6? (D) k>7?
3.设i为虚数单位,则 ( )
( )
(A)-2-3i (B)-2+3i (C)2-3i (D)2+3i
2. 已知函数
已知函数  若
若
 =( )
=( )
(A)0 (B)1 (C)2 (D)3
1.设 则
则 ( )
( )
(A) (B)
(B) (C)
(C) (D)
(D)
21、解法一:易知 所以
所以 ,设
,设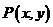 ,则
,则


故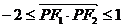 .…………2分
.…………2分
(2)显然直线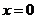 不满足题设条件,可设直线
不满足题设条件,可设直线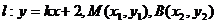 ,
,
联立 ,w.@w.w.k.&s.5*消去
,w.@w.w.k.&s.5*消去 ,整理得:
,整理得: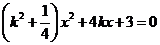 ………………………3分
………………………3分
∴
由 得:
得: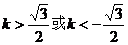 ………………………5分
………………………5分
又0°<∠MON<90°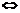 cos∠MON>0
cos∠MON>0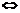
 >0 ∴
>0 ∴
又


∵ ,即
,即 ∴
∴
故由①、②得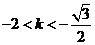 或
或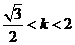 …………………………… ………………7分
…………………………… ………………7分
(3)解法一:根据点到直线的距离公式和①式知,点 到
到 的距离分别为
的距离分别为 ,
,
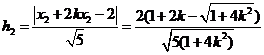 .……………………………………………9分
.……………………………………………9分
又 ,所以四边形
,所以四边形 的面积为
的面积为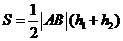 =
=


 ,
,
…………………………………………………11分
当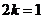 ,即当
,即当 时,上式取等号.所以
时,上式取等号.所以 的最大值为
的最大值为 .………12分
.………12分
解法二:由题设, ,
, .
.
设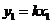 ,
, ,由①得
,由①得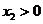 ,
,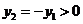 ,……………………9分
,……………………9分
故四边形 的面积为
的面积为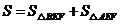



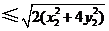
 ,…11分
,…11分
当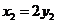 时,上式取等号.所以
时,上式取等号.所以 的最大值为
的最大值为 .…………………12分
.…………………12分
20、解:(1) ,……… 2分令
,……… 2分令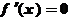 得
得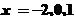 ,
,
|
x |
 |
-2 |
 |
0 |
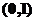 |
1 |
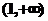 |
 |
- |
0 |
+ |
0 |
- |
0 |
+ |
 |
递减 |
极小值 |
递增 |
极大值 |
递减 |
极小值 |
递增 |
所以当 时
时 的极大值为
的极大值为 ;……………………………………………………4分
;……………………………………………………4分
(2)当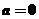 时,由(Ⅰ)知当
时,由(Ⅰ)知当 和
和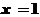 ,
, 分别取极小值
分别取极小值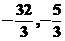 ,所以函数
,所以函数 的最小值为
的最小值为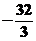 ,又当
,又当 时
时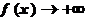 ,故函数
,故函数 的值域为
的值域为 ,8分
,8分
(3) 即
即 ,
,
记 ,
, 在
在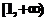 递增,只需
递增,只需 ,即
,即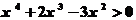 ,即
,即 ,解得
,解得 ,所以满足条件的
,所以满足条件的 的
的
取值范围是 …………………12分
…………………12分
19、解:(I)由图可知二次函数的图象过点(0,0),(1,0)
则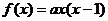 ,又因为图象过点(2,6)∴6=2a ∴a=3
,又因为图象过点(2,6)∴6=2a ∴a=3
∴函数 的解析式为
的解析式为
(Ⅱ)由 得
得
∵ ,∴直线
,∴直线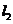 与
与 的图象的交点
的图象的交点
横坐标分别为0,1+t ,
由定积分的几何意义知:

 ,
, 
18、解法一:(I)由AC=1,AB= ,BC=
,BC= 知AC2+AB2=BC2,所以AC⊥AB。因为ABC-A1B1C1是直三棱柱,面ABB1A1⊥面ABC,所以AC⊥面ABB1A1。……3分
知AC2+AB2=BC2,所以AC⊥AB。因为ABC-A1B1C1是直三棱柱,面ABB1A1⊥面ABC,所以AC⊥面ABB1A1。……3分
由三垂线定理得A1B⊥B1C。 …………6分
(II)作BD⊥B1C,垂足为D,连结A1D。由(I)知,A1B⊥B1C,则B1C⊥面A1BD,
于是B1C⊥A1D, 则∠A1DB为二面角A1-B1C-B的平面角。……8分
 ∴Rt△A1B1C≌Rt△B1BC,
∴Rt△A1B1C≌Rt△B1BC,
 故二面角A1-B1C-B的大小为
故二面角A1-B1C-B的大小为
解法二:由AC=1,AB= ,BC=
,BC= 知AC2+AB2=BC2,
知AC2+AB2=BC2,
所以AC⊥AB。如图建立空间直角坐标系
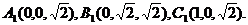 …2分(I)
…2分(I) 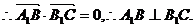 ……6分
……6分
(II)作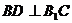 ,垂足为D,连结A1D。
,垂足为D,连结A1D。
设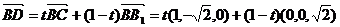
 ,
, 所以
所以 等于二面角A1-B1C-B的大小。
等于二面角A1-B1C-B的大小。
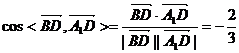 ,
,
故二面角A1-B1C-B的大小为 ………………12分
………………12分
(2) ,
,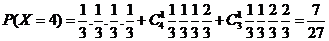

17、解 当n=1时, ,
,
即 , ∴a<26,又a∈
, ∴a<26,又a∈ ,∴取a=25,下面用数学归纳法证明:[
,∴取a=25,下面用数学归纳法证明:[
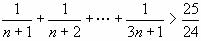 。… ………2分
。… ………2分
(1)当n=1时,已证。…………4分
(2)假设当n=k时,  成立。……6分
成立。……6分
则当n=k+1时,有


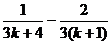 ,……………8分
,……………8分
∵ ,
,
∴ 也成立。……………10分
也成立。……………10分
由(1)、(2)可知,对一切n∈N*,都有不等式 成立。
成立。
∴a的最大值为25。………………12分
21、(14分) 设 、
、 分别是椭圆
分别是椭圆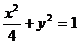 的左、右焦点.
的左、右焦点.
(1)若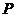 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
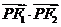 的取值范围;
的取值范围;
(2)设过定点Q(0,2)的直线 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.
(3)设 是它的两个顶点,直线
是它的两个顶点,直线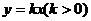 与AB相交于点D,与椭圆相交于E、F两点.求四边形
与AB相交于点D,与椭圆相交于E、F两点.求四边形 面积的最大值.
面积的最大值.
 岳口高中高二年级期末复习理科数学----五答案
岳口高中高二年级期末复习理科数学----五答案
BBADB BBABA
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com