3.　　　 (93上海)正方体ABCD－A′B′C′D′中，过顶点B、D、C′作截面，则二面角B－DC′－C的大小为____________

2.　　　 (89(18)4分)如图，已知圆柱的底面半径是3，高是4，A，B两点分别在两底的圆周上，并且AB＝5，那么直线AB与轴OO′之间的距离等于_________. 注:现行考试大纲指出：“对于异面直线的距离，只要求会计算已给出公垂线时的距离”。因此本题考察范围超出大纲要求。

1.　　　 (88(20)4分)如图，四棱锥S－ABCD的底面是边长为1的正方形，侧棱SB垂直于底面，并且SB＝，用α表示∠ASD，则sinα＝__________.

30．(2001上海(15))若有平面与，且，则下列命题中的假命题为(　　 )

A．过点且垂直于的直线平行于．　　　 B．过点且垂直于的平面垂直于． C．过点且垂直于的直线在内．　　　　 D．过点且垂直于的直线在内．

29.　 (2001北京(11)5分)右图是正方体的平面展开图，在这个正方体中，

①BM与ED平行 ②CN与BE是异面直线③CN与BM成角④DM与BN垂直

以上四个命题中，正确命题的序号是

(A)　　　　　　　　　　　　　　　　　　　　　　　　 ②③　 (B)②④　 (C)③④　 (D)②③④

28.　　 (2001(9)5分)在正三棱柱ABC-A₁B₁C₁中，若AB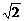＝BB₁，则AB₁与C₁B所成的角的大小为 A．60°　　　　　　 B．90°　　　　　　 C．105°　　　　　　 D．75°

27.　　 (98上海)在下列命题中，假命题是 A.若平面α内的一条直线l垂直于平面β内的任一直线，则α⊥β； B.若平面α内的任一直线平行于平面β，则α∥β； C.若平面α⊥平面β，任取直线l∩α，则必有l⊥β； D.若平面α∥平面β，任取直线l∩α，则必有l∥β

26.　　 (97(4)4分)已知三棱锥D－ABC的三个侧面与底面全等，且AB＝AC＝，BC＝2，则以BC为棱，以面BCD与面BCA为面的二面角的大小为 A.arccos　　　　 B.arccos　　　　 C.　　　　　　　　 D.

25.　　 (96上海)在下列命题中，真命题是 A.若直线m、n都平行于平面α，则m∥n； B.设α－l－β是直二面角，若直线m⊥l，则m⊥β； C.若直线m、n在平面α内的射影依次是一个点和一条直线，且m⊥n，则n在α内或n与α平行； D.设m、n是异面直线，若m与α平行，则n与α相交

24.　　 (96(5)4分)如果直线l、m与平面α、β、γ满足:l＝β∩g，l∥α，mÌα和m⊥g，那么必有 A.α⊥g且l⊥m　　　 B.α⊥g且m∥β　　 C.m∥β且l⊥m　　　 D.α∥β且α⊥g