
题目列表(包括答案和解析)
17. 解:(1)由 消去y得:
消去y得: ①
设
①
设 ,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
只需讨论以下三种情况:
1°△=0得:
,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
只需讨论以下三种情况:
1°△=0得: ,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
2°f
(a)f (-a)<0,当且仅当-a<m<a;
3°f
(-a)=0得m=a,此时xp=a-2a2,当且仅当-a<a-2a2<a,即0<a<1时适合.
f (a)=0得m=-a,此时xp=-a-2a2,由于-a-2a2<-a,从而m≠-a.
综上可知,当0<a<1时,
,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
2°f
(a)f (-a)<0,当且仅当-a<m<a;
3°f
(-a)=0得m=a,此时xp=a-2a2,当且仅当-a<a-2a2<a,即0<a<1时适合.
f (a)=0得m=-a,此时xp=-a-2a2,由于-a-2a2<-a,从而m≠-a.
综上可知,当0<a<1时, 或-a<m≤a;
当a≥1时,-a<m<a.
或-a<m≤a;
当a≥1时,-a<m<a.
(2)△OAP的面积 ∵0<a<
∵0<a< ,故-a<m≤a时,0<
,故-a<m≤a时,0< <a,
由唯一性得
<a,
由唯一性得  显然当m=a时,xp取值最小.由于xp>0,从而yp=
显然当m=a时,xp取值最小.由于xp>0,从而yp= 取值最大,此时
取值最大,此时 ,∴
,∴ .
当
.
当 时,xp=-a2,yp=
时,xp=-a2,yp=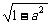 ,此时
,此时 .
下面比较
.
下面比较 与
与 的大小:
令
的大小:
令 ,得
,得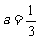 故当0<a≤
故当0<a≤ 时,
时, ≤
≤ ,此时
,此时 .
当
.
当 时,
时,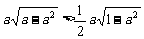 ,此时
,此时 .
.
16. 或
或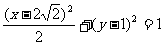
15.
14.1,3
13.解:设正方形的边AB在直线 上,而位于抛物线上的两个顶点坐标为
上,而位于抛物线上的两个顶点坐标为 、
、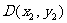 ,则CD所在直线
,则CD所在直线 的方程
的方程 将直线
将直线 的方程与抛物线方程联立,得
的方程与抛物线方程联立,得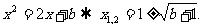
令正方形边长为 则
则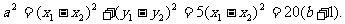 ①
①
在 上任取一点(6,,5),它到直线
上任取一点(6,,5),它到直线 的距离为
的距离为 ②.
②.
①、②联立解得 或
或
12.设椭圆的长轴、短轴的长及焦矩分别为2a、2b、2c,则由其方程知a=3,b=2,c= ,故,|PF1|+|PF2|=2a=6,又已知[PF1|:|PF2|=2:1,故可得|PFl|=4,|PF2|=2.在△PFlF2中,三边之长分别为2,4,2
,故,|PF1|+|PF2|=2a=6,又已知[PF1|:|PF2|=2:1,故可得|PFl|=4,|PF2|=2.在△PFlF2中,三边之长分别为2,4,2 ,而22+42=(2
,而22+42=(2 )2,可见△PFlF2是直角三角形,且两直角边的长为2和4,故△PFlF2的面积=4.
)2,可见△PFlF2是直角三角形,且两直角边的长为2和4,故△PFlF2的面积=4.
11.90º
1.C 2.B 3.B 4.B 5.B 6.A 7.C 8.B 9.D.10.D
20.过抛物线 上的一点A(1,1)作抛物线的切线,分别交
上的一点A(1,1)作抛物线的切线,分别交 轴于D,交
轴于D,交 轴于B.点C在抛物线上,点E在线段AC上,满足
轴于B.点C在抛物线上,点E在线段AC上,满足 ;点F在线段BC上,满足
;点F在线段BC上,满足 ,且
,且 ,线段CD与EF交于点P.当点C在抛物线上移动时,求点P的轨迹方程.
,线段CD与EF交于点P.当点C在抛物线上移动时,求点P的轨迹方程.
2005~2006年皖南十校期末联考
19.在平面直角坐标系xoy中,给定三点 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若直线L经过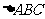 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com