
题目列表(包括答案和解析)
19.已知椭圆 ,其长轴长是短轴长的2倍,右准线方程为
,其长轴长是短轴长的2倍,右准线方程为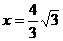 .
(1)求该椭圆方程,
(2)如过点(0,m),且倾斜角为
.
(1)求该椭圆方程,
(2)如过点(0,m),且倾斜角为 的直线l与椭圆交于A、B两点,当△AOB(O为原点)面积最大时,求m的值.
的直线l与椭圆交于A、B两点,当△AOB(O为原点)面积最大时,求m的值.
18.求过点P(1,6)与圆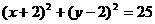 相切的直线方程.
相切的直线方程.
17.已知不等式 .(1)求a,b的值,
(2)解不等式
.(1)求a,b的值,
(2)解不等式 (c为常数).
(c为常数).
16.给出下列命题:
(1)角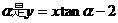 的倾斜角
的倾斜角
(2)若 的充要条件
的充要条件
(3)若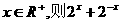 的最小值为2
的最小值为2
(4)若定义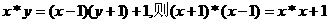
其中正确命题的序号是 .
15.F1,F2是双曲线 的两个焦点,P是双曲线上的点,已知|PF1|,|PF2|,|F1F2|依次成等差数列,且公差大于0,则∠F1PF2=
.
的两个焦点,P是双曲线上的点,已知|PF1|,|PF2|,|F1F2|依次成等差数列,且公差大于0,则∠F1PF2=
.
14.设椭圆 的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦长等于F1到l1的距离,则椭圆的离心率为
.
的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦长等于F1到l1的距离,则椭圆的离心率为
.
13.若不等式 ,则a=
.
,则a=
.
22.(本小题满分14分)已知抛物线 的弦AB与直线y=1有公共点,且弦AB的中点
的弦AB与直线y=1有公共点,且弦AB的中点
N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.

2003-2004学年度第一学期期末二省一市四校联考
21.(本小题满分12分)二次函数 ,已知
,已知 且
且 ;(1)求证:
;(1)求证: (2)求证:
(2)求证: ;(3)若
;(3)若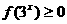 的解集是
的解集是 解析式.
解析式.
20.(本小题满分12分)某商场预计全年分批购入每台价值为2000元的电视机共3600台,
每批都购入x台(x是正整数),且每批均需付运费400元,储存购入的电视机全年所付
保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需
用去运费和保管费用43600元,现在全年只有24000元资金可以用于支付这笔费用,请
问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com