
题目列表(包括答案和解析)
10.若x>0,y>0且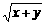 ≤a·(
≤a·(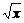 +
+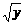 )成立,则a的最小值是( )
)成立,则a的最小值是( )
A. B.
B.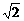 C.2 D.2
C.2 D.2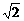
分析:本题主要考查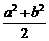 ≥(
≥(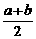 )2,参数隔离法.
)2,参数隔离法.
解:由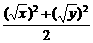 ≥(
≥(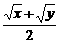 )2,
)2,
∴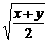 ≥
≥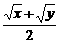 ,即a≥
,即a≥ ,amin=
,amin= .故应选A.
.故应选A.
答案:A
9.已知h>0,设甲:两实数a、b满足|a-b|<2h;乙:两实数a、b满足|a-1|<h且|b-1|<h,则( )
A.甲是乙的充分但不必要条件 B.甲是乙的必要但不充分条件
C.甲是乙的充要条件 D.甲既不是乙的充分条件,也不是乙的必要条件
分析:本题主要考查含绝对值不等式|a|-|b|≤|a±b|≤|a|+|b|,充要条件.
解:|a-b|=|(a-1)-(b-1)|≤|a-1|+|b-1|<2h.故应选B.
答案:B
8.一批救灾物资随26辆汽车从某市以v km/h速度匀速直达灾区,已知两地公路线长 400 km,为了安全起见,两辆汽车的间距不得小于(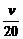 )2 km,那么这批物资全部到达灾区,最少需要( )
)2 km,那么这批物资全部到达灾区,最少需要( )
A.5 h B.10 h C.15 h D.20 h
解析:时间t=[400+25(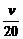 )2]÷v=
)2]÷v=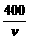 +
+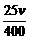
≥2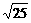 =10.
=10.
答案:B
7.函数f(x)=x+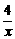 +3在(-∞,-2]上( )
+3在(-∞,-2]上( )
A.无最大值,有最小值7 B.无最大值,有最小值-1
C.有最大值7,有最小值-1 D.有最大值-1,无最小值
解析:f(x)=x+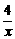 +3=-(-x+
+3=-(-x+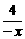 )+3≤-4+3=-1.
)+3≤-4+3=-1.
故选D.
答案:D
6.两次购买同一种物品,可以有两种不同的策略.第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.若两次购买这种物品时价格不相同,则两种策略中比较经济的情况为( )
A.第一种策略经济 B.第二种策略经济 C.两种策略同样经济 D.不能判断
分析:本题主要考查不等式的应用.本题关键是比较两种不同的购买方式的平均价格的 大小.
解:(1)按第一种策略购物,设第一次购物时价格为p1,购n(kg),第二次购物时价格为p2,仍购n(kg).按这种策略购物时两次购物的平均价格为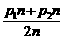 =
=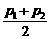 .
.
(2)若按第二种策略购物,第一次花m元钱,能购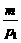 (kg)物品,第二次仍花m元钱,能购
(kg)物品,第二次仍花m元钱,能购 (kg)物品,两次购物的平均价格为
(kg)物品,两次购物的平均价格为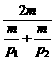 =
= .
.
比较两次购物的平均价格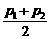 -
-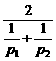 =
=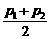 -
-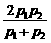
=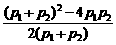 =
=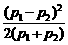 >0(∵p1≠p2),
>0(∵p1≠p2),
∴第一种策略的平均价格高于第二种策略的平均价格.
因而,用第二种策略比较经济.
答案:B
5.下列命题中,真命题有( )
①若a+b>0且ab>0,则a>0且b>0 ②若a>b且ab>0,则a>b>0
③若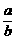 >
>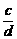
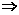 ad>bc
④a>b是
ad>bc
④a>b是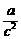 >
>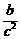 成立的必要条件
成立的必要条件
A.①③ B.②③ C.②④ D.①④
分析:本题主要考查不等式的性质,用排除法.
解:∵ab>0,∴a、b同号.又a+b>0,
∴a>0且b>0.①正确,排除B、C.
由③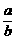 -
-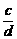 >0,得
>0,得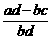 >0,不能保证ad>bc.③不正确.故应选D.
>0,不能保证ad>bc.③不正确.故应选D.
答案:D
4.角x,y满足-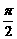 <x<y<
<x<y<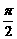 ,则x-y的取值范围是( )
,则x-y的取值范围是( )
A.(-π,0) B.(-π,π) C.(-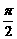 ,0) D.(-
,0) D.(-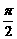 ,
,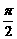 )
)
分析:本题主要考查负数在不等式中的变化,不等式的性质.
解:由x<y,得x-y<0.又-π<x-y<π,
∴-π<x-y<0.
答案:A
3.若a>b>1,P=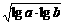 ,Q=
,Q=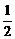 (lga+lgb),R=lg(
(lga+lgb),R=lg(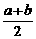 ),则( )
),则( )
A.R<P<Q B.P<Q<R C.Q<P<R D.P<R<Q
分析:本题主要考查均值不等式与对数函数的单调性.
解:a>b>1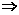 lga>0,lgb>0.
lga>0,lgb>0.
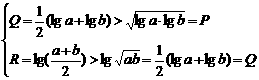
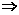
R>Q>P.
答案:B
2.若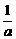 <
<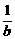 <0,则下列不等式:①a+b<ab;②|a|>|b|;③a<b;④
<0,则下列不等式:①a+b<ab;②|a|>|b|;③a<b;④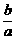 +
+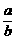 >2.正确的不等式有( )
>2.正确的不等式有( )
A.1个 B.2个 C.3个 D.4个
分析:本题主要考查不等式的性质及均值不等式的适用条件.
解:由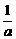 <
<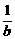 <0可知b<a<0,③不正确,②不正确.
<0可知b<a<0,③不正确,②不正确.
∴a+b<0,ab>0.∴a+b<ab,①正确.
由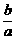 >0,
>0, 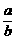 >0,而a≠b,∴
>0,而a≠b,∴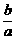 +
+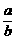 >2,④正确.
>2,④正确.
答案:B
1.若a、b、c为实数,则下列命题正确的是( )
A.若a>b,则ac2>bc2 B.若a<b<0,则a2>ab>b2
C.若a<b<0,则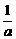 <
<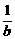 D.若a<b<0,则
D.若a<b<0,则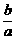 >
>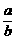
解析:A.因为c2≥0,所以只有c≠0时才正确.c=0时,ac2=bc2,所以A是假命题.
变式:若ac2>bc2,则a>b,命题是真命题.
B.a<b,a<0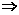 a2>ab,a<b,b<0
a2>ab,a<b,b<0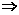 ab>b2,B是真命题.
ab>b2,B是真命题.
C.由性质定理a<b<0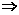
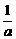 >
>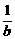 ,C是假命题.
,C是假命题.
D.例如-3<-2<0, <
<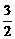 ,D是假命题.
,D是假命题.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com