5、长方体共顶点的三条棱长分别是、、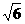，则长方体的体对角线长为_____。

4、点A(3, –4)关于点M(–4, 3)的对称点B的坐标是 　　　　　　　。

3、设集合M = {正方体}，N = {直四棱柱}，P = {正四棱柱}，Q = {直平行六面体}，则四个集合间的包含关系是　 　　　　　　　　　　　　　　　。

2、直线y=x+1的倾斜角为 　　　　　　　。

1、两条异面直线所成角的范围是　　　　　　　　 。

28、在底半径为r的圆柱中,O、O′分别为上下底面圆的圆心，OM和O′N′分别为上下底面圆的两条半径，若异面直线OM和O′N′的成角为60^o.求：异面直线MN′和OO′的距离。

27、完成下列证明：已知a∥b∥c，a∩d=A，b∩d=B，c∩d=C，求证：a、b、c、d共面。

证明：∵a//b，∴___确定一个平面a，∵AÎa，BÎb.

　　 　∴A__a，B__a，又∵AÎd，BÎd，∴___Ìa.同理dÌ(b、c确定的平面)b.

　　　 ∵b、dÌ___，且b、dÌ__，bId=B，∴__与__重合，∴____共面。

说明：立几中证n条直线共面，一般可根据条件先确定一个平面(根据公理三及三推论)，然后再证其它直线也在这个平面内；也可先确定n个平面，再证这些平面重合。翰林汇

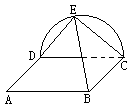
26、已知ABCD为矩形，E为半圆CED上一点，且平面ABCD⊥平面CDE.

(1)求证：DE是AD与BE的公垂线；

(2)若AD=DE=，求AD和BE所成角的大小。

　　　　　　　　　 翰林汇

25、已知两个全等的正方形ABCD和CDEF所在平面互相垂直。

(1)求BD与EC所成的角；

(2)若P，Q分别为两个正方形的中心，求BQ与EP所成角的余弦值。

　　　　　　　　　 翰林汇

24、已知异面直线a，b互相垂直，它们的公垂线段PQ=h，一条长为定值m(m＞h)的线段AB两端分别在a，b 上滑动，求AB中点M的轨迹。翰林汇