
题目列表(包括答案和解析)
2.已知点P是直线l:2x-y-4=0与x轴的交点,把直线绕点P按逆时针方向旋转 ,得到的直线方程是( )
,得到的直线方程是( )
A、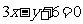 B、
B、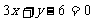 C、
C、 D、
D、
1..已知直线l1:(a+1)x+y-2=0与直线l2:ax+(2a+2)y+1=0互相垂直,则实数a的值
为( )
A.-1或2 B. 1或2 C. -1或-2 D.1或-2
11.甲、乙两人独立解某一道数学题,已知该题被甲独立解出的概率为 ,被甲解出而乙解不出的概率为
,被甲解出而乙解不出的概率为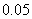 。
。
(1)求该题被乙独立解出的概率;
(2)求恰有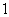 人能解出这道题目的概率。
人能解出这道题目的概率。
答案  (2)
(2) 。
。
10.在 个大小相同的均匀的球中,有白球
个大小相同的均匀的球中,有白球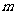 个。
个。
(1)不放回地逐个抽取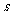 个小球,求其中恰有
个小球,求其中恰有 个白球的概率;
个白球的概率;
(2)每次抽取后又放回地逐个抽取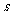 个小球,求其中恰有
个小球,求其中恰有 个白球的概率。
个白球的概率。
解  ;
;
9.设掷一颗均匀的正方体玩具两次,此玩具的六个表面分别刻有数字 。
。
求掷得的点数之和小于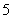 的概率。
的概率。
解 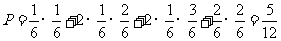 。
。
8.甲、乙两人参加一次测试,已知在备选的 道试题中,甲能答对其中的
道试题中,甲能答对其中的 道题,乙能答对其中的
道题,乙能答对其中的 道题,规定每次测试都从备选题中随机抽取出
道题,规定每次测试都从备选题中随机抽取出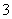 题进行测试,至少答对
题进行测试,至少答对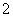 题才算合格。
题才算合格。
(1)分别求甲、乙两人测试合格的概率;
(2)求甲、乙两人中至少有一人考试合格的概率。
解 (1)甲合格的概率为 ,乙合格的概率为
,乙合格的概率为 ;
;
(2)两人中至少有一人合格的概率为 。
。
7.已知从甲地到乙地的海底光缆有 个接点,其中有一个接点发生故障,为了及时排除故障,需要尽快断定故障发生点。以
个接点,其中有一个接点发生故障,为了及时排除故障,需要尽快断定故障发生点。以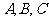 三个接点为例,检查接点
三个接点为例,检查接点 的方法如下:在接点
的方法如下:在接点 处分别检查
处分别检查 两段,若两段都有问题,则可断定
两段,若两段都有问题,则可断定 点存在问题;若只有一段存在问题,则接点正常。设至少需要检查的接点数为
点存在问题;若只有一段存在问题,则接点正常。设至少需要检查的接点数为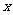 个,则
个,则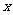 的最大值为
。(
的最大值为
。(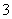 )
)
6.抛掷一枚硬币若干次,每次正面向上得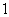 分,反面向上得
分,反面向上得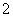 分。
分。
则恰好得到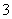 分的概率为 。(
分的概率为 。( )
)
5.口袋内装有 个相同的小球,其中
个相同的小球,其中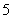 个小球标有数字
个小球标有数字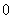 ,
,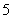 个小球标有数字
个小球标有数字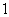 。若从中摸出
。若从中摸出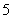 的小球,那么摸出的
的小球,那么摸出的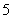 个小球所标数字之和小于
个小球所标数字之和小于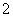 或大于
或大于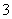 的概率是
。(
的概率是
。( )
)
4.在 世纪的一天,保罗与梅尔进行赌钱游戏。每人拿出
世纪的一天,保罗与梅尔进行赌钱游戏。每人拿出 枚金币,然后玩骰子,约定谁先胜三局谁就得到
枚金币,然后玩骰子,约定谁先胜三局谁就得到 枚金币(每局均有胜负)。比赛开始后,保罗胜了一局,梅尔胜了两局,这时一件意外的事情中断了比赛,于是他们商量这
枚金币(每局均有胜负)。比赛开始后,保罗胜了一局,梅尔胜了两局,这时一件意外的事情中断了比赛,于是他们商量这 枚金币应该怎样分配才合理。据此,你认为合理的分配方案是保罗和梅尔分别得到金币
(
枚金币应该怎样分配才合理。据此,你认为合理的分配方案是保罗和梅尔分别得到金币
(  )
)
 枚,
枚, 枚
枚  枚,
枚, 枚
枚 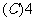 枚,
枚, 枚
枚  枚,
枚,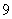 枚
枚
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com