
题目列表(包括答案和解析)
5、在正方体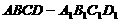 中,点
中,点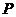 为棱
为棱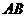 上的一动点,则
上的一动点,则 与
与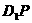 所成的角为( )
所成的角为( )
A 随点 的变化而变化 B 45° C
的变化而变化 B 45° C  D
D 
4.已知α,β是平面,m、n、 是直线.下列命题中不正确的是
( )
是直线.下列命题中不正确的是
( )
A 若m∥n,m⊥α,则n⊥α B 若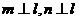 ,则m∥n
,则m∥n
C 若m⊥α,m⊥β,则α∥β D 若m⊥α,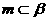 ,则α⊥β
,则α⊥β
3.由0,1,2,3组成的无重复数字的四位数一共有 ( )
A 6个 B 18个 C 24 个 D 28个
2.在正多面体中没有( )
A 正六面体 B 正八面体 C 正十二面体 D 正十六面体
1.经过空间任意三点的平面 ( )
A 只有一个 B 有二个
C 有无数多个 D 只有一个或有无数多个
21.设函数f(x)=  a
a R.(1)当a =1时,求证f(x)为单调增函数;
R.(1)当a =1时,求证f(x)为单调增函数;
(2)当x [1,3]时,f (x)的最小值为4,求a的值。
[1,3]时,f (x)的最小值为4,求a的值。
20. 高三(1)班50名学生在元旦联欢时,仅买了甲、乙两种饮料可供饮用,在联欢会上甲饮料喝掉了36瓶,乙饮料喝掉了39瓶,假设每个人至多喝一瓶甲饮料和一瓶乙饮料,并且有5名学生两种饮料都没有喝,随机选取该班的一名学生,计算下列事件的概率
(1) 他没有喝甲饮料;
(2) 他喝了1瓶乙饮料但是没有喝甲饮料;
(3) 他喝了1瓶甲饮料和1瓶乙饮料。
19.美国篮球职业联赛(NBA)某赛季在湖人队与活塞队之间进行,比赛采取七局四胜制,即有一队胜四场,则此队获胜且比赛结束.因两队实力非常接近,在每场比赛中每队获胜是等可能的. 据资料统计,每场比赛组织者可获门票收入100万美元. 问:
(1) 组织者在此次决赛中获门票收入恰为400万美元的概率为多少?
(2) 组织者在此次决赛中获门票收入不少于600万美元的概率是多少?
18.如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC =900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.(Ⅰ)求证:DF∥平面ABC;(Ⅱ)求二面角B-AD-C的大小;(Ⅲ)求AB与平面BDF所成角的大小.

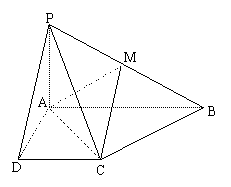
17.已知四棱锥 的底面是直角梯形,
的底面是直角梯形, 底面ABCD,
底面ABCD, 是PB的中点.(I)证明:平面
是PB的中点.(I)证明:平面 平面PCD;(II)求AC与PB所成的角;(III)求平面AMC与平面BMC所成角的大小.
平面PCD;(II)求AC与PB所成的角;(III)求平面AMC与平面BMC所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com