1．双曲线的渐近线方程是　　　　　　　　　　　 (　　　 )

　　　　 A．　　　　 B．　　　　 C．　　　　 D．

22．(本题14分)如图,四棱锥P-ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD.

(1)求证：平面PAC⊥平面PBD；

(2)求PC与平面PBD所成的角；

(3)在线段PB上是否存在一点E，

使得PC⊥平面ADE？若存在，请加

以证明，并求此时二面角A-ED-B

的大小；若不存在，请说明理由。

21．(本题13分)如图，将长，宽AA₁＝3的矩形沿长的三等分线处折迭成一个三棱柱，如图所示：

(1)求平面APQ与底面ABC所成二面角的正切值；

(2)求三棱锥A₁－APQ的体积.

20．(本题13分)如图，△ABC中，AC＝BC，AE和CD都垂直于平面ABC，且AE＝AB＝2，F为BE的中点，DF∥平面ABC，

(1)求CD的长；

(2)求证：AF⊥BD；

(3)求平面EDB与平面ABC所成的二面角的大小．

19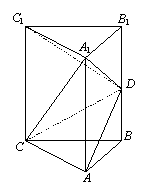．(本题12分)如图，直三棱柱ABC－A₁B₁C₁中，AB＝AC＝AA₁，

∠BAC＝90⁰，D为棱BB₁的中点．

　 (1)求异面直线C₁D与A₁C所成的角；

(2)求证：平面A₁DC⊥平面ADC．

18．(本题12分)在四棱锥P－ABCD中，底面ABCD是矩形，AB＝，

AD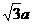＝，PA⊥平面ABCD，PA＝，Q为PA的中点

(1)求Q到BD的距离；

(2)求P到平面BQD的距离。

17．(本题10分)已知PA垂直于矩形ABCD所在平面，M、N分别是AB、PC的中点

求证：MN⊥AB

16．如图，四棱柱ABCD－A₁B₁C₁D₁中，给出三个结论：

①四棱柱ABCD－A₁B₁C₁D₁为直四棱柱；

②底面ABCD为菱形；

③AC₁⊥B₁D₁．

以其中两个论断作为条件，余下的一个论断作为结论，

可以得到三个命题，其中正确命题的个数为　　　　 ．

三：解答题(共计74分)

15．三棱锥P－ABC的四个顶点在同一球面上, 若PA⊥底面ABC，底面ABC是直角三角形，PA＝2，AC＝BC＝1，则此球的表面积为　　　　　　　

14．已知正四棱锥P－ABCD的高为4，侧棱与底面所成的角为60⁰，则该正四棱锥的侧面积是　　　　　　　　　　 ．