20．解：设动点M(x，y)，动直线l：y=x+m，并设P(x₁，y₁)，Q(x₂，y₂)是方程组的解，消去y，得3x²+4mx+2m²-4=0，其Δ=16m²-12(2m²-4)>0，∴-<m<，x₁+x₂=-，

x₁x₂=，故|MP|=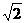|x-x₁|，|MQ|=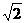|x-x₂|．由|MP||MQ|=2，得|x-x₁||x-x₂|=1，也即|x²-(x₁+x₂)x+x₁x₂|=1，于是有|x²++|=1．∵m=y-x，∴|x²+2y²-4|=3．由x²+2y²-4=3，得椭圆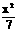+=1夹在直线y=x±间两段弧，且不包含端点．由x²+2y²-4=-3，得椭圆x²+2y²=1．

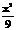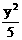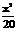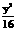19．解：由+=1，得F₁(2，0)，F₂(-2，0)，F₁关于直线l的对称点F₁^/(6，4)，连F₁^/F₂交l于一点，即为所求的点M，∴2a=|MF₁|+|MF₂|=|F₁^/F₂|=4，∴a=2，又c=2，∴b²=16，故所求椭圆方程为+=1．

18．解：(1)直线AB的方程为y=-x+2；　 (2)所求椭圆的方程为+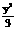=1．

22．(本小题满分14分)

已知椭圆的一个顶点为A(0，－1)，焦点在x轴上，若右焦点到直线x－y+2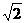＝0的距离为3．

(1)求椭圆的方程；

(2)设椭圆与直线y＝kx+m(k≠0)相交于不同的两点M、N，当｜AM｜＝｜AN｜时，求m的取值范围．

单元六

21．(本小题满分12分)

设椭圆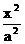+=1的两焦点为F₁、F₂，长轴两端点为A₁、A₂．

(1)　　　 P是椭圆上一点，且∠F₁PF₂=60⁰，求ΔF₁PF₂的面积；

(2)　　　 若椭圆上存在一点Q，使∠A₁QA₂=120⁰，求椭圆离心率e的取值范围．

20．(本小题满分12分)

一条变动的直线l与椭圆+=1交于P、Q两点，M是l上的动点，满足关系|MP|·|MQ|=2．若直线l在变动过程中始终保持其斜率等于1．求动点M的轨迹方程，并说明曲线的形状．

19．(本小题满分12分)

已知+=1的焦点F₁、F₂，在直线l：x+y-6=0上找一点M，求以F₁、F₂为焦点，通过点M且长轴最短的椭圆方程．

18．(本小题满分12分)

设中心在原点，焦点在x轴上的椭圆的离心率为，并且椭圆与圆x²+y²-4x-2y+=0交于A、B两点，若线段AB的长等于圆的直径．

(1)　　　 求直线AB的方程；

(2)　　　 求椭圆的方程．

17．(本小题满分12分)

已知A、B为椭圆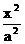+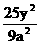=1上两点，F₂为椭圆的右焦点，若|AF₂|+|BF₂|=a，AB中点到椭圆左准线的距离为，求该椭圆方程．

16．过椭圆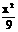+=1的左焦点作一条长为的弦AB，将椭圆绕其左准线旋转一周，则

弦AB扫过的面积为　　　　 ．