5．球的体积是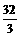π，则此球的表面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

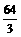　　　 A． 12π　 　　　　　　 B． 16π　　 　　　　　 C． π　　 　　　　 D． π

4．球面上有3点，其中任意两点的球面距离都等于大圆周长的，经过这3点的小圆的周长为 ，那么这个球的半径为 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　 　　　　　　　 B． 　　　　　　　 C． 2　　 　　　　　　　 D．

3．下列四个命题中，其中错误的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 ①经过球面上任意两点，可以作且只可以作一个大圆；

　 ②经过球直径的三等分点，作垂直于该直径的两个平面，则这两个平面把球面分成三部分的面积相等；

　 ③球的面积是它大圆面积的四倍；

　 ④球面上两点的球面距离，是这两点所在截面圆上，以这两点为端点的劣弧的长。

　　　 A． 0　　　 　　　　　　 B． 1 　　　　　　　　 C． 2　　　 　　　　　 D． 3

2．球的体积是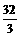π，则此球的表面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

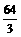　　　 A． 12π　 　　　　　　 B． 16π　　 　　　　　 C． π　　 　　　　 D． π

1．下列命题①多面体的面数最少为4；②正多面体只有5种；③凸多面体是简单多面体；④一个几何体的表面，经过连续变形为球面的多面体就叫简单多面体。其中正确的个数为(　　 )

　　　 A．1　　 　　　　　　　　　 B．2 　　　　　　　　　 C．3　　 　　　　　　　 D．4

22. (14′)(理)一名学生骑自行车上学,从家到学校的途中共有6个交通岗,假设他在各个交通岗遇到红灯的概率事件相互独立,且概率都是.

①　　 设ξ为这名学生在途中遇到红灯的次数,求ξ的分布列;

②　　 设η为这名学生在首次停车前经过的路口数,求η的分布列;

③　　 求这名学生在途中至少遇到一次红灯的概率.

(文)已知两家工厂上半年每月工业生产产值如下表(单位:万元)

试分析两厂家的生产情况.

21. (12′)(理)如图所示:甲、乙两个工厂,甲厂位于一条直线河岸的岸边的A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此河岸边合建一个供水站C,从供水站到甲厂和两厂的水管费用为每千米3a元,5a元,问供水站C建在岸边何处才能使水管费用最省?

(文)已知f(x)=x³+bx²+cx+d在(-∞,0)上是增函数,在[0,2]上是减函数,且方程f(x)=0有三个根,它们分别是:

①　　 求c的值;②求证: f(1)≥2;③求∣∣的取值范围.

20. (12′)(理)设,问:a、b为何值时,f(x)在定义区间内连续?

(文)某的现有耕地面积10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%,若人口增长率为1%,那么耕地面积平均每年至多只能减少多少公顷(精确到1.0)?

(粮食单产=,人均粮食占有量=).

19. (12′)已知曲线f(x)=x³+px²+qx的图像与x轴相切于异于原点的的一点,又函数有极小值-4.

求f(x)的单调区间.

18. (12′) (理)平面内有n条直线,其中无任何两条平行,也无任何三条共点.

求证:这n条直线把平面分割成块.

(文)甲、乙二人投篮,投中的概率分别为0.6,0.7,今各投3次,

求:甲比乙投中次数多的概率.