18． (2+)R

解： 将四个球心两两连结(2分)，构成一个棱长为2R的正四面体(4分)

设底面正三角形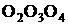的中心为H, 则(8分)

　(10分)

故上层小球最高处离桌面的距离为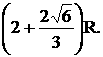(12分)

17． 解：由题意知，光线与地面成60°角(2 分)，设球的阴影部分面积为S，垂直于光线的大圆面积为

S′(6分)，则Scos30°＝S′(9分),并且S′＝9π，所以S＝6π(米²)…… 12分

16．解　 设球的半径为R，依题意知截面圆的半径r＝12,球心与截面的距离为d＝R-8，由截面性质得：r²+d²＝R²,即12²+(R-8)²＝R²．　　 得R＝13　 ∴该球半径为13cm．

13．　 14．　 15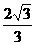． 　　16．13cm．

9．解：球的体积等于水下降的体积即，。答案：D

8．解：设球心为O，纬度为的纬线圈的圆心为O´，则∠O´AO=,∴O´A=OAcos∠O´AO=Rcos,设A,B两地间的径度差的弧度数为，则

Rcos=,　 ∴=,　 即A,B两地是⊙O´的一条直径的两端点，∴∠AOB=,　

∴A,B两地之间的球面距离为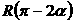．　 答案：D

1．D　 2．B　 3．C　 4．B　 5．B　 6．A　 7．C　 8．D　 9．D 10．C　 11．D　 12． B

1解：据多面体的概念选D

6解：已该正四面体的六条棱为面对角线的正方体的棱长为1，这里的正四面体与正方体的外接球相同，故其外接球的直径为，其表面积为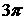。选A．

7解： = =．

　　　 = , =

∴=,　 >．选C．

(五)

17．(12分)在有阳光时，一根长为3米的旗轩垂直于水平地面，它的影长为米，同时将一个半径为3米的球放在这块水平地面上，如图所示，求球的阴影部分的面积(结果用无理数表示)．

18．(12分) 把四个半径为R的小球放在桌面上，使下层三个，上层一个，两两相切，求上层小球最高处离桌面的距离．

19．(12分)A、B、C是球O表面上三点，AB=6㎝，∠ACB= 30°，点O到△ABC所在截面的距离为5㎝，求球O的表面积。

20．(12分)如果球、正方体与等边圆柱(底面直径与母线相等)的体积相等，求它们的表面积的大小关系。

21．(12分)球O的半径为R,A﹑B﹑C在球面上，A与B,A与C的球面距离都为，B与C的球面距离为，求球O在二面角B-OA-C内的部分的体积。

22．(14分)同底的两个正三棱锥内接于半径为R的球，它们的侧面与底面所成的角分别为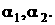求：(1)侧面积的比； (2)体积的比；(3)角的最大值。

16．湖结冰时，一个球漂在其上，取出后(未弄破冰)，

冰面上留下了一个直径为24cm,深为8cm的空穴，

则该球的半径为