分析、启发、讲练结合．

3．疑点：推导l1、l2的角公式时的构图的分类依据．

1．重点：前面研究了两条直线平行与垂直，本课时是对两直线相交的情况作定量的研究．两直线所成的角公式可由一条直线到另一条直线的角公式直接得到，教学时要讲请l1、l2的公式的推导方法及这一公式的应用．

2，难点：公式的记忆与应用．

(三)学科渗透点

训练学生由特殊到一般，定性、定量逐步深入地研究问题的习惯．

(二)能力训练点

通过课题的引入，训练学生由特殊到一般，定性、定量逐层深入研究问题的思想方法；通过公式的推导，培养学生综合运用知识解决问题的能力．

(一)知识教学点

一条直线与另一条直线所成角的概念及其公式，两直线的夹角公式，能熟练运用公式解题．

20. 已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为。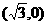

　　 (1) 求双曲线C的方程；

(2) 若直线l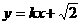：与双曲线C恒有两个不同的交点A和B，且(其中O为原点)，求k的取值范围。

19.已知p：|l-|≤2；q：x²-2x+l-m²≤0(m>0)，若¬p是¬q的必要而不充分条件，求实数m的取值范围．

18. 设0<a,b,c<1,用反证法证明: (1-a)b,(1-b)c,(1-c)a不同时大于

17. 如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点.

　 (Ⅰ)求直线AC与PB所成角的余弦值；

(Ⅱ)在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离.