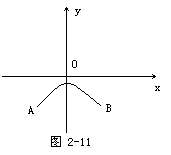
4．如图2-11建立坐标系，得拱圆的方程：

x2+(y+27.88)2=27.882(-7.2≤y≤0)

2．因为直径的端点为A(x1，y1)、B(x2，y2)，则圆心和半径分别为

所以圆的方程为

化简得：x2-(x1+x2)x+x1x2+y2-(y1+y2)y+y1y2=0

即(x-x1)(x-x2)+(y-y1)(y-y2)=0

1．(1)(x-3)2+(y+5)2= 32

4．赵州桥的跨度是37.4m，圆拱高约为7.2m，求这座圆拱桥的拱圆的方程．

作业答案：

3．一个等腰三角形底边上的高等于5，底边两端点的坐标是(-4，0)和(4，0)，求它的外接圆的方程．

2．已知：一个圆的直径端点是A(x1，y1)、B(x2，y2)．

证明：圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0．

1．求下列条件所决定的圆的方程：

(1)圆心为 C(3，-5)，并且与直线x-7y+2=0相切；

(2)过点A(3，2)，圆心在直线y=2x上，且与直线y=2x+5相切．

(四)本课小结

1．圆的方程的推导步骤；

2．圆的方程的特点：点(a，b)、r分别表示圆心坐标和圆的半径；

3．求圆的方程的两种方法：(1)待定系数法；(2)轨迹法．

(二)建立圆的标准方程

1．建系设点

由学生在黑板上画出直角坐标系，并问有无不同建立坐标系的方法．教师指出：这两种建立坐标系的方法都对，原点在圆心这是特殊情况，现在仅就一般情况推导．因为C是定点，可设C(a，b)、半径r，且设圆上任一点M坐标为(x，y)．

2．写点集

根据定义，圆就是集合P={M||MC|=r}．

3．列方程

由两点间的距离公式得：

4．化简方程

将上式两边平方得：

(x-a)2+(y-b)2=r2．

(1)

方程(1)就是圆心是C(a，b)、半径是r的圆的方程．我们把它叫做圆的标准方程．

这时，请大家思考下面一个问题．

问题5：圆的方程形式有什么特点？当圆心在原点时，圆的方程是什么？

这是二元二次方程，展开后没有xy项，括号内变数x，y的系数都是1．点(a，b)、r分别表示圆心的坐标和圆的半径．当圆心在原点即C(0，0)时，方程为 x2+y2=r2．

教师指出：圆心和半径分别确定了圆的位置和大小，从而确定了圆，所以，只要a，b，r三个量确定了且r＞0，圆的方程就给定了．这就是说要确定圆的方程，必须具备三个独立的条件．注意，确定a、b、r，可以根据条件，利用待定系数法来解决．