
题目列表(包括答案和解析)
3.如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a=
(A)-3 (B)-6
(C)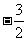 (D)
(D)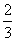
2.设a、b为实数,且a+b=3,则 的最小值为( )
的最小值为( )
(A)6 (B)
(C) (D)8
(D)8
1.已知实数a、b、c满足b+c=6-4a+3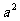 ,c-b=4-4a+
,c-b=4-4a+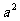 ,则a、b、c的大小
,则a、b、c的大小
关系是( ).
(A)c≥b>a (B)a>c≥b
(C)c>b>a (D)a>c>b
22、(本小题满分14分)
解:(1)如图所示,利用Rt△AOC和Rt△AOD可求得OC=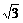 (公里),
(公里),
OD= (公里)…………………………………………2分
(公里)…………………………………………2分
在△ODC中,由余弦定理,得
CD =OC
=OC +OD
+OD -2·OC·ODcos120°
-2·OC·ODcos120°
 =(
=(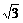 )
) +(
+( )
) -2
-2 ·
· (-
(- )=
)=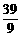
∴DC= (公里)……………………………………4分
(公里)……………………………………4分
∴v= =6·DC=6
=6·DC=6 =2
=2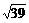 (公里/小时)…………6分
(公里/小时)…………6分
(2) 如图所示,过C作CF∥OD,则∠CFE=∠DOE=30°
∴CO=CF= ……………………8分
……………………8分
而△OED∽△FEC
∴ =
=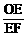 ,即
,即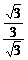 =
=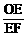 ∴OE=
∴OE= EF
EF
作CM⊥OF,则OM= OF
OF
于是 OE=OM=MF
在Rt△OMC中,OM=OC·cos30°
∴OE= OF=OM=OC·cos30°=
OF=OM=OC·cos30°= ·
·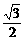 =
=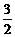 (公里)…………10分
(公里)…………10分
在△EOC中,由余弦定理,得
CE =OE
=OE +OC
+OC -2·OE·OCcos150°
-2·OE·OCcos150°
=( )
) +(
+( )
) -2·
-2· ·
· (-
(-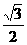 )=
)=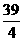
∴CE= …………………………………………………………12分
…………………………………………………………12分
∴t=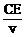 =
=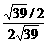 =
= (小时)
(小时)
因此,若船的速度不变,11点15分船可到达岛的正西方向,此时所在点E距岛1.5公里。……………………………………………………………………14分
21、(本小题满分12分)
证法1:(1)连结OB ,
,
∵OO ⊥平面AOB,∴OO
⊥平面AOB,∴OO ⊥AO
⊥AO
即AO⊥OO ,又AO⊥OB
,又AO⊥OB
∴AO⊥平面OO B
B B
B
∴O B 为A B
为A B 在平面OO
在平面OO B
B B内的射影…2分
B内的射影…2分
又OB=B B ∴四边形OO
∴四边形OO B
B B为正方形
B为正方形
∴B O ⊥OB
⊥OB
∴B O ⊥A B
⊥A B (三垂线定理)………………………………4分
(三垂线定理)………………………………4分
(2)连结A O 交OA
交OA 于E,再连结DE.
于E,再连结DE.
∵四边形AA O
O O为矩形 ,∴E为A O
O为矩形 ,∴E为A O 的中点.
的中点.
又D为AB的中点,∴BO ∥DE…………………………6分
∥DE…………………………6分
又DE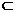 平面OA
平面OA D,BO
D,BO
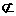 平面OA
平面OA D
D
∴BO ∥平面OA
∥平面OA D…………………………………………8分
D…………………………………………8分
(3)令B点到平面OA D的距离为h
D的距离为h
∵OA =2
=2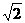 ,A
,A D=
D= ,OD=
,OD=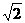 ∴OD
∴OD + A
+ A D
D = OA
= OA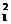
∴△A DO为Rt△
∴S
DO为Rt△
∴S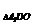 =
= ·A
·A D·OD=
D·OD=
∴V =
= ·S
·S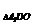 ·h=
·h=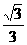 h………………………………10分
h………………………………10分
又S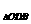 =
= ·S
·S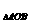 =1
=1
∴V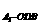 =
= ·S
·S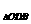 ·A
·A A=
A= ×1×2=
×1×2=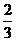
又V =V
=V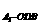 ∴
∴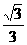 h=
h=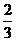 ∴h=
∴h=
即B点到平面OA D的距离为
D的距离为 .……………………12分
.……………………12分
证法2:以O 为原点建立如图所示的空间直角坐标系,则:
为原点建立如图所示的空间直角坐标系,则:
O (0,0,0),A
(0,0,0),A (2,0,0),B
(2,0,0),B (0,2,0),A(2,0,2),
(0,2,0),A(2,0,2),
B(0,2,2), O(0,0,2), D(1,1,2).…………………………………2分
⑴∵ =(-2,2,-2),
=(-2,2,-2),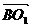 =(0,-2,-2)
=(0,-2,-2)
∴ ·
·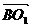 =(-2) ·0+2·(-2)+(-2) ·(-2)=0
=(-2) ·0+2·(-2)+(-2) ·(-2)=0
∴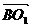 ⊥
⊥ ∴B O
∴B O ⊥A B
⊥A B ……………………4分
……………………4分
⑵取OA 的中点为E,则E点的坐标是(1,0,1),
的中点为E,则E点的坐标是(1,0,1),
∴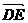 =(0,-1,-1), 又
=(0,-1,-1), 又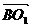 =(0,-2,-2)
=(0,-2,-2)
∴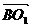 =2
=2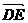 又BO
又BO 、DE不共线,
、DE不共线,
∴BO ∥DE……………………………………………………6分
∥DE……………………………………………………6分
又DE 平面OA
平面OA D,BO
D,BO
 平面OA
平面OA D
D
∴BO ∥平面OA
∥平面OA D……………………………………………8分
D……………………………………………8分
⑶令平面OA D的法向量为
D的法向量为 =(x,y,z),
=(x,y,z),
则 ⊥
⊥ ,
, ⊥
⊥ ∴
∴ ·
· =0,
=0,  ·
· =0
=0
又 =(-2,0,2)
=(-2,0,2)  =(-1,1,2)
=(-1,1,2)
∴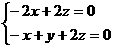
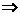

取 =(1,-1,1)
………………………………………………10分
=(1,-1,1)
………………………………………………10分
又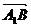 =(-2,2,2)
=(-2,2,2)
∴B点到平面OA D的距离为:
D的距离为: =
=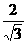 =
=  …………12分
…………12分
20、(本小题满分12分)
解:(1)∵q≠1 ∴a =
= …………………………………………2分
…………………………………………2分
于是A =
=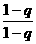 C
C +
+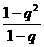 C
C +…+
+…+ C
C
= [(C
[(C +C
+C +…+C
+…+C )-(C
)-(C q+C
q+C q
q +…+C
+…+C q
q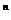 )]……………4分
)]……………4分
= [(C
[(C +C
+C +…+C
+…+C )-(C
)-(C +C
+C q+…+C
q+…+C q
q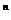 )]
)]
= [2
[2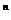 -(1+q)
-(1+q)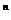 ](q≠1).……………………………………………6分
](q≠1).……………………………………………6分
(2)b +b
+b +…+b
+…+b =
= [1-(
[1-(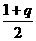 )
)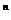 ]
]
b +b
+b +…+b
+…+b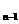 =
= [1-(
[1-(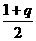 )
) ] (n
] (n N
N ,n³2)
,n³2)
相减得:b =
= [(
[(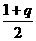 )
) -(
-(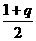 )
) ]……………………………8分
]……………………………8分
= (
(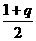 )
) (
(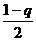 )
)
= (
(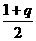 )
) (n
(n N
N ,n³2)
,n³2)
又b1= ,则:b
,则:b
 (
(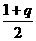 )
) (n
(n N
N )…………………………10分
)…………………………10分
∴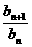 =
=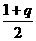 (q≠-1)
(q≠-1)
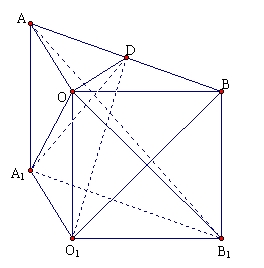 ∴{b
∴{b }是等比数列.…………………………………………………12分
}是等比数列.…………………………………………………12分
19、(本小题满分12分)
解:记甲、乙两人独立地破译出密码的事件分别是A、B,则P(A)= ,
,
P(B)= …………………………………………………………3分
…………………………………………………………3分
(1)甲、乙两人都译不出密码的概率为:
P(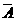 ·
·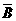 )=P(
)=P(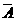 )·P(
)·P(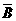 )=(1-
)=(1- )(1-
)(1- )=
)= …………………………6分
…………………………6分
(2)甲、乙两人中恰有一人能译出密码的概率为:
P(A·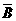 +B·
+B·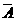 )=P(A·
)=P(A·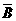 )+P(B·
)+P(B·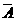 )=
)= (1-
(1- )+
)+ (1-
(1- )=
)= ……9分
……9分
(3)甲、乙两人中至多有一人能译出密码的概率为:
1- P(A·B)=1- ×
× =
= ……………………………………………12分
……………………………………………12分
18、(本小题满分12分)
证法1:作AO⊥平面BCD于O,则BO、CO、DO分别为AB、AC、AD在平面BCD内的射影.……………………………………………………3分
∵CD⊥AB,CD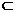 平面BCD
平面BCD
∴CD⊥BO(三垂线定理的逆定理)…………6分
同理BC⊥DO
∴O为△BCD的垂心…………………………9分
从而BD⊥CO
∴BD⊥AC(三垂线定理),即AC⊥BD…………12分
证法2:作出向量 、
、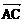 、
、 、
、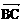 、
、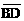 、
、 .
.
∵ ⊥
⊥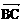 ,
, ⊥
⊥
∴ ·
·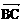 =0,
=0, ·
· =0…………………………………4分
=0…………………………………4分
又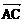 =
= +
+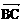 ,
,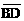 =
=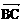 +
+
∴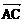 ·
·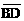 =
= ·
·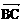 +
+ ·
· +
+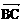
 +
+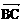 ·
· …………8分
…………8分
= ·
· +
+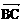 (
( +
+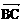 +
+ )
)
= ·
· +
+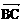 ·
· =0
=0
∴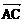 ⊥
⊥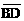 ∴AC⊥BD……………………………………12分
∴AC⊥BD……………………………………12分
17、(本小题满分12分)
解:⑴记事件A为从男、女学生13人中任选出两人的性别相同,
即P(A)= ,
,
则事件 为从男、女学生13人中任选出两人的性别不同,…………3分
为从男、女学生13人中任选出两人的性别不同,…………3分
则P( )=1- P(A)=1-
)=1- P(A)=1- =
= 。……………………………………5分
。……………………………………5分
⑵设该班男生有x人,则女生有(13-x)人,( 0£x£13,xÎN)………6分
则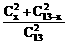 =
= ,………………………………………………………9分
,………………………………………………………9分
得x2-13x+40=0,解得x=8或x=5,………………………………………11分
故该班男生有8人,女生有5人;或该班男生有5人,女生有8人。…12分
13、0.5 14、129 15、8 16、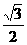
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com