
题目列表(包括答案和解析)
9. 满足不等式 –
– <
< 的最小正整数x等于
的最小正整数x等于
(A)5. (B) 9 . (C) 24 . (D) 25.
8. 抛物线的顶点在原点, 对称轴为坐标轴, 焦点是直线 3x + 5y – 15 = 0与y轴的交点, 那么抛物线的方程是
(A) x 2 = 12y . (B) y 2 = 10x . (C) y 2 = 20x . (D) x 2 = 6y.
7.点P (0 , 1 )在直线ax + y – b = 0上的射影是点Q ( 1 , 0 ), 则a , b的值依次是
(A) –1 , 1 . (B) –1, –1. (C) 1 , 1. (D) 1, –1.
6. 已知实数对 ( x , y ) 满足x 2 + y 2 £ 1 且y ³ 0, 则y – x的取值范围是
(A) [ – 1 , 1 ] (B)[ 0 , 1] (C) [– 1 ,  ]
(D)[–
]
(D)[– ,
, ]
]
5. 已知q Î[ – p,p], 则点P (1 , 1 )到直线 xcosq + ysinq = 2的最大距离为
(A) 2. (B) .
(C)2 –
.
(C)2 –
 . (D) 2 +
. (D) 2 + .
.
4. 设直线2x – y – = 0与y轴交于P点, 则点P将圆 ( x + 1 )
2 + y 2 = 25的直径分为两段的长度之比为
= 0与y轴交于P点, 则点P将圆 ( x + 1 )
2 + y 2 = 25的直径分为两段的长度之比为
(A)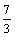 或
或 . (B)
. (B) 或
或 .
(C)
.
(C) 或
或 . (D)
. (D) 或
或 .
.
3. 若2 +| m |与|m| – 3 异号,则m的取值范围是
(A) m > 3. (B) –3< m < 3. (C) 2 < m < 3. (D) m< –2或– 3 < m < 2, 或m > 3.
2. 双曲线 的焦点坐标是
的焦点坐标是
(A)(-2,0),(2,0). (B)(0,-2),(0,2).
(C)(0,-4),(0,4). (D)(-4,0),(4,0).
1. 若a>b,c ÎR,则下列命题中成立的是
(A) . . (B)
. . (B)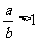 .
(C)
.
(C)  . (D)
. (D) .
.
20. (本小题满分12分)
某游泳馆出售学生游泳卡,每张240元,使用规定:不记名,每卡每次只限1人,每天只限一次. 某班有48名学生, 老师打算组织同学们集体去游泳, 且要求每位学生能游8次.在费用开支方面, 除需购买x张游泳卡外, 每天游泳还要包一辆汽车, 无论乘坐多少名学生. 每次包车费均为40元.
(1)试写出游泳活动总开支y元关于购买游泳卡张数x 的函数解析式;
(2)试求出购买多少张游泳卡,可以使每位同学需要交纳的费用最少? 最少需要交多少元?
21 附加题: (本题分值6分, 计入总分, 但本题与必做题得分之和不超过100分.)
 (附加题) |
已知a , b都是正数,△ABC是平面直角坐标系xOy内, 以两点A ( a , 0 )和B ( 0 , b )为顶点的正三角形,且它的第三个顶点C在第一象限内.
(1)若△ABC能含于正方形D = { ( x , y ) | 0 £ x £ 1, 0£ y £ 1}内, 试求 变量 a , b 的约束条件,并在直角坐标系aOb内(见答题卷)内画出这个约束等条件表示的平面区域;
(2)当( a, b )在(1)所得的约束条件内移动时,求△ABC面积S的最大值,并求此时(a , b )的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com