
题目列表(包括答案和解析)
7.设坐标原点为O,抛物线 与过焦点的直线交于A、B两点,则
与过焦点的直线交于A、B两点,则 等于( )
等于( )
(A) (B)
(B) (C)3 (D)-3
(C)3 (D)-3
6.与圆 外切又与
外切又与 内切的圆的圆心的轨迹足( )
内切的圆的圆心的轨迹足( )
(A)两个椭圆 (B)双曲线的一支 (C)双曲线 (D)双曲线的一支和一条直线
5.圆 与直线
与直线 的位置关系是( )
的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)不确定
4. 某汽车运输公司,购买了一批豪华大客车投入营运,据市场分析
某汽车运输公司,购买了一批豪华大客车投入营运,据市场分析
每辆客车营运的总利润 (亿元)与营运年数
(亿元)与营运年数 为二次函数关
为二次函数关
系如图示,则每辆客车营运多少年,其营运的年平均利润最大?( )
(A)3 (B)4 (C)5 (D)6
3.对于直线 ,其倾斜角的取值范围是( )
,其倾斜角的取值范围是( )
(A) (B)
(B) (C)
(C) (D)
(D)
2.一个直角三角形的周长为 ,其斜边长的最小值是( )
,其斜边长的最小值是( )
(1)1 (B)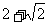 (C)2 (D)
(C)2 (D)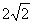
1.若 ,则下列不等式均成立的是( )
,则下列不等式均成立的是( )
(A)
(B)
(C)
(D)
22.(14分)一束光线以M(-3,2)射向直线l:x-2y-3=0,经l反射后通过点N(1,3),在其反射光线所在的直线上求一点Q,使Q到A(8,5)的距离与到B(4,1)的距离之差最大。
解:第一步.求M关于l的对称点M’ (1,-6) ···········3分
第二步求直线M’N的方程 :x=1 ···········6分
第三步求直线AB的方程: x-y-3=0 ···········10分
第四步求AB与M’N的交点Q(1,-2) ···········14分
21.(12分)过点P(2,1),作直线l交x轴,y轴的正向于A、B两点,求
(1)ΔAOB面积最小时直线l的方程。
(2)|PA|·|PB|最小时的直线l的方程。
解:设l的斜率为k , 则其方程为: y-1=k (x-2 ) , 则 A (2- ,0) B ( 0 ,1-2k )
,0) B ( 0 ,1-2k )
 2
-
2
- >0
>0
1-2k>0  k<0 ············2分
k<0 ············2分
<1> s= |2 -
|2 - |·|1-2k|=
|·|1-2k|=
 化简得 4
化简得 4 +2(s-2)k+1=0
+2(s-2)k+1=0
 由
由
 0 得s
0 得s 4 (或s
4 (或s 0舍) 当
0舍) 当 AOB面积最小时, 即s=4时 求得k=
AOB面积最小时, 即s=4时 求得k=
l的方程为: x+2y-4=0 ············7分
<2> P(2,1), A (2- ,0) , B ( 0 ,1-2k ) 则 ,|PA|= ,|PB|=
|PA||PB|==≥4,取等号时,k2=,即k=-1,
l的方程为: :x+y-3=0
另:<2> |PA|=| | , |PB|=|
| , |PB|=| | , |PA|·|PB| =|
| , |PA|·|PB| =| |=
|=
0<|sin2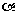 |
| 1
1
 |PA|·|PB|
|PA|·|PB| 4 取等号时2
4 取等号时2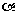 =
= ,
,
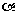 =
=
 k=-1
k=-1
l的方程为: :x+y-3=0 ············12分
20、(12分)某工厂用两种不同原料均可生产同一产品,若采用甲种原料,1吨成本1000元,运费500元,可得产品90kg。若采用乙种原料1吨成本1500元,运费400元,可得产品100kg。若每日预算总成本不得超过6000元,运费不得超过2000元,问工厂每日最多可生产多少kg产品?
解:设工厂每日需要甲种原料x吨,乙种原料y吨,可得产品z=90x+100y (㎏) ······2分

 x
x 0 x
0 x 0
0
又 y 0
y
0
y 0
0
1000x+1500y 6000
6000  2x+3y
2x+3y 12 ············6分
12 ············6分
500x+400y 2000
5x+4y
2000
5x+4y 20
20

 画出可行域,不难求出最优解为
(
画出可行域,不难求出最优解为
( ) ··········11分
) ··········11分
5
z=90×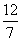 +100×
+100× =440
=440
4
答:每日最多生产440㎏ ············12分


o 4 6 x
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com