5．设F₁, F₂是椭圆的两个焦点，P在椭圆上，已知P, F₁, F₂是一个Rt△的三个顶点，且|P F₁|>|P F₂|，则|P F₁| : |P F₂|的值是　　　　　　　　　　　　　　　　 (　　 )

　 (A)或2　 　(B)或　 　(C)或　 　(D)或2

4．“ab<0”是“方程ax²+by²=c表示双曲线”的　　　　　　　　　　 　　　　　( 　　)

　 (A)必要不充分条件　 　　　　　　　　(B)充分不必要条件

　 (C)充要条件　　　 　　　　　　　　　(D)非充分非必要条件

3．椭圆的两个焦点和中心把两准线间的距离四等分，则一焦点与短轴两端点连线的夹角是　　　　　　　　　　　　　　　　　　　　　　　　　 　　

　 (A)　　　 (B)　　　 (C)　　　 (D)　　　 　　　　　　　　( 　　)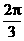

2．椭圆(1－m)x²－my²=1的长轴长是　　　　　　　　　　　　　　　 　　　　　(　 　　)

(A)　　 (B)　　 (C)　　 (D)

1．圆x²+y²+2x+6y+9＝0与圆x²+y²－6x+2y+1＝0的位置关系是　 　　　　　( 　　)

(A)相离　 (B)相外切　 (C)相交　 (D)相内切

22．(本题14分)

注：文科做(1)(2)理科做(1)(2)(3)

如图,四棱锥P-ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD.

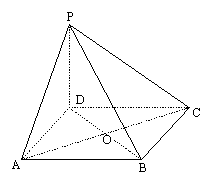(1)求证：平面PAC⊥平面PBD；

(2)求PC与平面PBD所成的角；

(3)在线段PB上是否存在一点E，

使得PC⊥平面ADE？若存在，请加

以证明，若不存在，请说明理由。

19．(本小题满分12分)

如图，在四棱锥中，底面ABCD是正方形，侧棱底面ABCD，

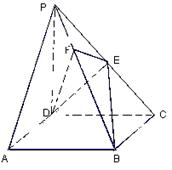
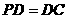　 　　　 ，E是PC的中点，作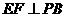交PB于点F.

　 (1)证明 平面；

　 (2)证明平面EFD．

20．(本小题满分12分)

如图，在直三棱柱ABC-A₁B₁C₁中， AA₁=4，AB=5，BC=3，AC=4，D为CC₁的中点。

(1)求异面直线AD与A₁B₁所成角的余弦值；

(2)试在线段AB上找一点E，使得：A₁E⊥AD；

18、．(本小题满分12分)

设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

(1)只有一个盒子空着，共有多少种投放方法？

(2)没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

　 (3)每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

19　 在长方体ABCD-A₁B₁C₁D₁中，AB=4，BC=3，　 　　　　　CC₁=2，如图　 　　

(1)　 求平面A₁BC₁与平面ACD₁间的距离；

(2) 求点B₁到平面A₁BC1的距离　

17．(本小题满分12分)

如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，E是DC的中点，取如图所示的空间直角坐标系．

　 (1)写出A、B₁、E、D₁的坐标；

　 (2)求AB₁与D₁E所成的角的余弦值．