
题目列表(包括答案和解析)
2. 三角与复数
例5 如果函数y = sin2x + a cos2x的图象关于x= 对称,则a=( ).
对称,则a=( ).
A.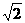 B.-
B.-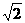 C. 1
D. -1
C. 1
D. -1
讲解 因为点(0,0)与点(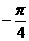 ,0)关于直线x=
,0)关于直线x= 对称,所以a必满足:
对称,所以a必满足:
sin0 + a cos0=sin( )+ a cos(
)+ a cos( ),
),
解出a=-1,从而可以排除A, B, C.,故应选D.
例6 在 内,使
内,使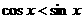 成立的
成立的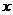 的取值范围是( ).
的取值范围是( ).
A. 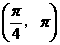 B.
B. 
C. 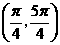 D.
D. 
讲解 将原不等式转化为 由
由 ,知
,知 ,从而
,从而 ,故应选C.
,故应选C.
事实上,由 显然满足
显然满足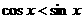 ,从而否定A, B, D, 故应选C.
,从而否定A, B, D, 故应选C.
亦可在同一坐标系中,作出函数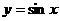 和
和 在
在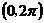 上的图象,进行直观求解.
上的图象,进行直观求解.
例7 复数 在复平面上对应的点不可能位于( ).
在复平面上对应的点不可能位于( ).
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
讲解 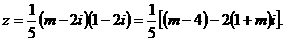
由 无解,可知应选A.
无解,可知应选A.
亦可取特值进行排除.事实上
记复数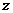 对应的点为P.若取
对应的点为P.若取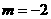 ,点P在第二象限;若取
,点P在第二象限;若取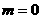 ,则点P在第三象限; 若取
,则点P在第三象限; 若取 ,则点P在第四象限,故应选A.
,则点P在第四象限,故应选A.
例8 把曲线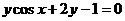 先沿
先沿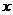 轴向右平移
轴向右平移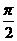 个单位,再沿
个单位,再沿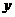 轴向下平移1个单位,得到的曲线方程是( ).
轴向下平移1个单位,得到的曲线方程是( ).
A.  B.
B. 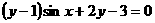
C.  D.
D. 
讲解 对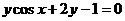 作变换
作变换

得
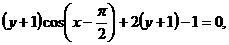
即  .
.
故应选C.
记住一些运动变换的小结论是有效的.本题是函数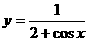 向方程式的变式,较为新颖.
向方程式的变式,较为新颖.
1. 函数与不等式
例1
已知 则
则 的值等于( ).
的值等于( ).
A. 0
B.  C.
C. 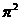 D. 9
D. 9
讲解 由 ,可知选C.
,可知选C.
例2 函数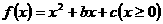 是单调函数的充要条件是( ).
是单调函数的充要条件是( ).
A. B.
B. C.
C.  D.
D. 
讲解 抛物线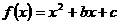 的开口向上,其对称轴为
的开口向上,其对称轴为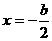 ,于是有
,于是有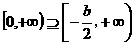 是递增区间,从而
是递增区间,从而 即
即 应选A.
应选A.
例3 不等式 的解集是( ).
的解集是( ).
A. 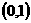 B.
B.  C.
C.  D.
D. 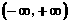
讲解 当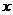 与
与 异号时,有
异号时,有 , 则必有
, 则必有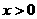 ,从而
,从而 ,解出
,解出 ,故应选A.
,故应选A.
例4
关于函数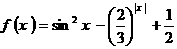 ,有下面四个结论:
,有下面四个结论:
(1)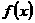 是奇函数;
是奇函数;
(2)当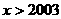 时,
时,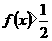 恒成立;
恒成立;
(3) 的最大值是
的最大值是 ;
;
(4)  的最小值是
的最小值是 .
.
其中正确结论的个数是( ).
A. 1个 B. 2个 C. 3个 D. 4个
讲解 由 是偶函数,可知(1)错;
是偶函数,可知(1)错;
又当 时,
时, ,所以错(2);
,所以错(2);
当 ,故(3)错;
,故(3)错;
从而对照选支应选A.
4. 解析几何
例18
直线 被抛物线
被抛物线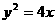 截得线段的中点坐标是___________.
截得线段的中点坐标是___________.
讲解 由 消去y,化简得
消去y,化简得
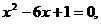
设此方程二根为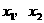 ,所截线段的中点坐标为
,所截线段的中点坐标为 ,则
,则
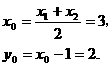
故 应填
 .
.
例19 椭圆 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解 记椭圆的二焦点为 ,有
,有
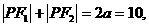
则知

显然当 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填 或
或
例20 一只酒杯的轴截面是抛物线的一部分,它的函数解析式是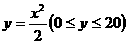 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
讲解 依抛物线的对称性可知,大圆的圆心在y轴上,并且圆与抛物线切于抛物线的顶点,从而可设大圆的方程为 
由

消去x,得 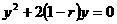 (*)
(*)
解出  或
或
要使(*)式有且只有一个实数根 ,只要且只需要
,只要且只需要 即
即
再结合半径 ,故应填
,故应填

填空题的类型一般可分为:完形填空题、多选填空题、条件与结论开放的填空题. 这说明了填空题是数学高考命题改革的试验田,创新型的填空题将会不断出现. 因此,我们在备考时,既要把关注这一新动向,又要做好应试的技能准备.
高考数学选择题怎么选
解答高考数学选择题既要求准确破解,又要快速选择,正如《考试说明》中明确指出的,应“多一点想的,少一点算的”,该算不算,巧判关. 因而,在解答时应该突出一个"选"字,尽量减少书写解题过程,在对照选支的同时,多方考虑间接解法,依据题目的具体特点,灵活、巧妙、快速地选择巧法,以便快速智取. 下面按知识版块加以例说.
4. 立体几何
例15 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径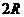 , 即有
, 即有

从而 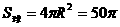 ,故应填
,故应填
例16 若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是 (只需写出一个可能的值).
讲解 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
 ,
,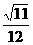 ,
,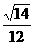 ,故应填.
,故应填. 、
、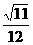 、
、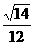 中的一个即可.
中的一个即可.
 例17 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
例17 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
3. 数列、排列组合与二项式定理
例10 已知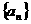 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果 是
是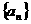 的前n项和,那么
的前n项和,那么

讲解 特别取 ,有
,有 ,于是有
,于是有
 故应填2.
故应填2.
例11
数列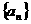 中,
中,
 , 则
, 则

讲解 分类求和,得


 ,故应填
,故应填 .
.
例12 有以下四个命题:
①
②
③凸n边形内角和为 ④凸n边形对角线的条数是
④凸n边形对角线的条数是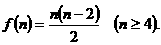
其中满足“假设 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当 (
( 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时,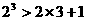 ,不等式成立;
,不等式成立;
② 当n=1时, ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
 ;
;
③  ,但假设
,但假设 成立,则
成立,则
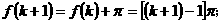
④ 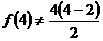 ,假设
,假设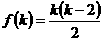 成立,则
成立,则
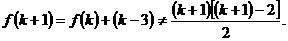
故应填②③.
例13 某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
讲解 中奖号码的排列方法是: 奇位数字上排不同的奇数有 种方法,偶位数字上排偶数的方法有
种方法,偶位数字上排偶数的方法有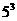 ,从而中奖号码共有
,从而中奖号码共有 种,于是中奖面为
种,于是中奖面为
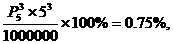
故应填
例14  的展开式中
的展开式中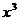 的系数是
的系数是
讲解 由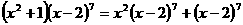 知,所求系数应为
知,所求系数应为 的x项的系数与
的x项的系数与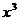 项的系数的和,即有
项的系数的和,即有
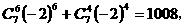
故应填1008.
2. 三角与复数
例5 已知点P 在第三象限,则角
在第三象限,则角 的终边在第
的终边在第 象限.
象限.
讲解 由已知得
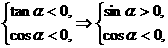
从而角 的终边在第二象限,故应填二.
的终边在第二象限,故应填二.
例6 不等式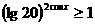 (
( )的解集为
)的解集为 .
.
讲解 注意到 ,于是原不等式可变形为
,于是原不等式可变形为

而 ,所以
,所以 ,故应填
,故应填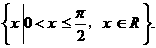
例7 如果函数 的图象关于直线
的图象关于直线 对称,那么
对称,那么
讲解 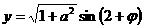 ,其中
,其中 .
.

 是已知函数的对称轴,
是已知函数的对称轴,
 ,
,
即  ,
,
于是  故应填
故应填 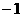 .
.
在解题的过程中,我们用到如下小结论:
函数 和
和 的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
例8 设复数 在复平面上对应向量
在复平面上对应向量 ,
, 将
将 按顺时针方向旋转
按顺时针方向旋转 后得到向量
后得到向量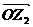 ,
,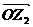 对应的复数为
对应的复数为 ,则
,则
讲解 应用复数乘法的几何意义,得

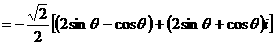 ,
,
于是 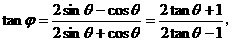
故应填 
例9 设非零复数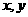 满足
满足 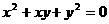 ,则代数式
,则代数式 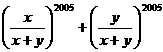 的值是____________.
的值是____________.
讲解 将已知方程变形为  ,
,
解这个一元二次方程,得
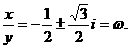
显然有 , 而
, 而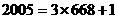 ,于是
,于是
原式=
=
=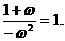
在上述解法中,“两边同除”的手法达到了集中变量的目的,这是减少变元的一个上策,值得重视.
1. 函数与不等式
例1 已知函数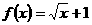 ,则
,则
讲解 由 ,得
,得
 ,应填4.
,应填4.
请思考为什么不必求 呢?
呢?
例2 集合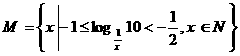 的真子集的个数是
的真子集的个数是
讲解  ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是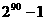 ,应填
,应填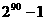 .
.
快速解答此题需要记住小结论;对于含有n个元素的有限集合,其真子集的个数是
例3 若函数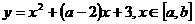 的图象关于直线
的图象关于直线 对称,则
对称,则
讲解 由已知抛物线的对称轴为 ,得
,得 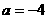 ,而
,而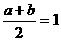 ,有
,有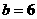 ,故应填6.
,故应填6.
例4 如果函数 ,那么
,那么
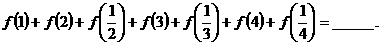
讲解 容易发现 ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式= ,应填
,应填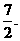
本题是2002年全国高考题,十分有趣的是,2003年上海春考题中也有一道类似题:
设 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得
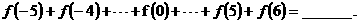
5、已知
(1)若 ,
,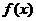 在
在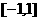 上的最大值为2,最小值为
上的最大值为2,最小值为 ,证明:
,证明: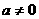 且
且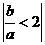 。
。
(2)若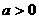 ,
, 是满足
是满足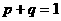 的实数,且对任意的实数
的实数,且对任意的实数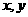 均满足
均满足 ,证明:
,证明: 。
。
高考数学填空题怎么填
填空题是数学高考的三种基本题型之一,其求解方法分为:直接运算推理法、赋值计算法、规律发现法、数形互助法等等. 解题时,要有合理的分析和判断,要求推理、运算的每一步骤都正确无误,还要求将答案表达得准确、完整. 合情推理、优化思路、少算多思将是快速、准确地解答填空题的基本要求. 下面将按知识分类加以例说.
4、二次函数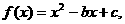 若
若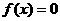 的根在
的根在 内,
内,
(1)求证: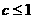 ; (2)
; (2)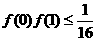
(3)若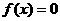 有一个根为
有一个根为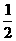 ,且当
,且当 时,
时,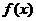 的最大值为M,求证:
的最大值为M,求证: 。
。
3、已知二次函数: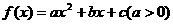 的图象与
的图象与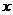 轴有两个不同的公共点,若
轴有两个不同的公共点,若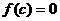 ,且
,且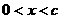 时,
时,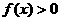 ;
;
(1)比较 与
与 的大小; (2)证明:
的大小; (2)证明: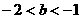 ;
;
(3)当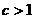 时,求证:
时,求证:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com