
题目列表(包括答案和解析)
6.设有编号为1,2,3,4,5的五个茶杯和编号为1,2,3,4,5的五个杯盖,将五个杯盖盖在五个茶杯上,至少有两个杯盖和茶杯的编号相同的盖法有-----------------------( )
A.30种 B.31种 C.32种 D.36种
5.(1-x)2n -1展开式中,二项式系数最大的项是---------------------------------( )
A.第n-1项 B.第n项 C.第n-1项与第n+1项 D.第n项与第n+1项
4.从正方体的六个面中选取3个面,其中有2个面不相邻的选法共有------------------------( )
A.8 B.12 C.16 D.20
3.某班举行联欢会,原定的五个节目已排出节目单,演出前又增加了两个节目,若将这两个节目插入原节目单中,则不同的插法总数为-----------------------------------------------------------------( )
A.42 B.36 C.30 D.12
2.在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是 ---------------------------------------------------------------------------------------------------------------( )
A.  B.C
B.C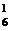 C
C C.C
C.C -C
-C D.A
D.A -A
-A
1.n∈N*,则(20-n)(21-n)……(100-n)等于----------------------------------------------------------( )
A.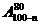 B.
B. C.
C. D.
D.
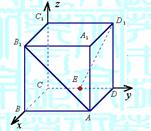 16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,
16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,
E是DC的中点,取如图所示的空间直角坐标系.
(1)写出A、B1、E、D1的坐标;
(2)求AB1与D1E所成的角的余弦值.
解:(1) A(2, 2, 0),B1(2, 0, 2),E(0, 1, 0),D1(0, 2, 2)
(2)∵ =(0, -2, 2),=(0, 1, 2) ∴ ||=2,||=,·=0-2+4=2,
∴ cos á,ñ = = = .∴ AB1与ED1所成的角的余弦值为.
17.(12分)在正方体 中, E、F分别是
中, E、F分别是
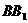 ,CD的中点,
,CD的中点,
(1)求证: 平面ADE;
平面ADE;
(2)求 .
.
解:建立如图所示的直角坐标系,(1)不妨设正方体的棱长为1,
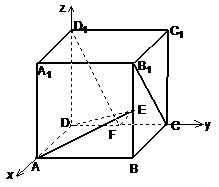 则D(0,0,0),A(1,0,0),
则D(0,0,0),A(1,0,0), (0,0,1),
(0,0,1),
E(1,1,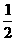 ),F(0,
),F(0,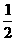 ,0),
,0),
则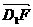 =(0,
=(0,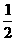 ,-1),
,-1), =(1,0,0),
=(1,0,0),
 =(0,1,
=(0,1,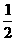 ),
则
),
则 =0,
=0,
 =0,
=0,  ,
, .
.
 平面ADE.
平面ADE.
(2) (1,1,1),C(0,1,0),故
(1,1,1),C(0,1,0),故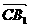 =(1,0,1),
=(1,0,1),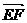 =(-1,-
=(-1,-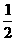 ,-
,-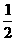 ),
),
 =-1+0-
=-1+0-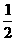 =-
=- ,
, 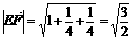 ,
,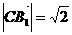 ,
,
则cos .
. 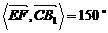 .
.
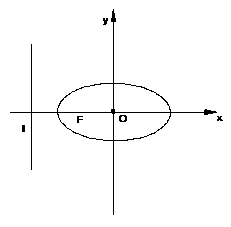 18,(本小题满分12分) 已知椭圆
18,(本小题满分12分) 已知椭圆 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线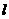 相切的圆的方程;
相切的圆的方程;
(II)设过点F的直线交椭圆于A、B两点,并且线段AB的
中点在直线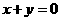 上,求直线AB的方程。
上,求直线AB的方程。

19,设双曲线 上两点A、B,AB中点M(1,2)
上两点A、B,AB中点M(1,2)
(1)求直线AB方程;
(2)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D是否共圆,为什么?
(1)显然AB斜率存在
设AB:y-2=k(x-1)
由 得:(2-k2)x2-2k(2-k)x-k2+4k-6=0
得:(2-k2)x2-2k(2-k)x-k2+4k-6=0
当△>0时,设A(x1,y1),B(x2,y2)
则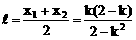
∴ k=1,满足△>0
∴ 直线AB:y=x+1
法二:设A(x1,y1),B(x2,y2)
则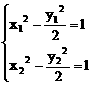
两式相减得:(x1-x2)(x1+x2)= (y1-y2)(y1+y2)
(y1-y2)(y1+y2)
∵ x1≠x2
∴ 
∴ 
∴ AB:y=x+1
代入 得:△>0
得:△>0
设A、B、C、D共圆于⊙OM,因AB为弦,故M在AB垂直平分线即CD上;又CD为弦,故圆心M为CD中点。因此只需证CD中点M满足|MA|=|MB|=|MC|=|MD|
由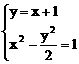 得:A(-1,0),B(3,4)
得:A(-1,0),B(3,4)
又CD方程:y=-x+3
由 得:x2+6x-11=0
得:x2+6x-11=0
设C(x3,y3),D(x4,y4),CD中点M(x0,y0)
则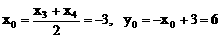
∴ M(-3,6)
∴ |MC|=|MD|= |CD|=
|CD|=
又|MA|=|MB|=
∴ |MA|=|MB|=|MC|=|MD|
∴ A、B、C、D在以CD中点,M(-3,6)为圆心, 为半径的圆上
为半径的圆上
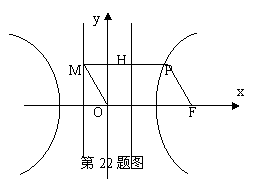
20,(本大题满分14分)如图,F为双曲线C: 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形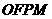 为平行四边形,
为平行四边形, 。
。
 (Ⅰ)写出双曲线C的离心率
(Ⅰ)写出双曲线C的离心率 与
与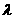 的关系式;
的关系式;
(Ⅱ)当 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。
,求此时的双曲线方程。
解:∵四边形 是
是 ,∴
,∴ ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则 ,又
,又 ,
, 。
。
(Ⅱ) 
14.设| |=1,|
|=1,| |=2,2
|=2,2 +
+ 与
与 -3
-3 垂直,
垂直, =4
=4 -
- ,
,
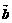 =7
=7 +2
+2 , 则<
, 则< ,
,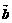 >=
0
>=
0
15,高5米和3m的旗竿在水平地面上,如果把两旗竿底部的坐标分别定为A(-5,0),B(5,0),则地面上杆顶仰角相等的点的轨迹是__________。

12.已知S是△ABC所在平面外一点,D是SC的中点,
若 =
= ,则x+y+z=
. 0
,则x+y+z=
. 0
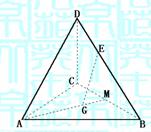 13.在空间四边形ABCD中,AC和BD为对角线,
13.在空间四边形ABCD中,AC和BD为对角线,
G为△ABC的重心,E是BD上一点,BE=3ED,
以{ ,
,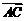 ,
, }为基底,则
}为基底,则 =
.
=
.
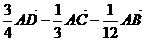
11.若A(m+1,n-1,3),B(2m,n,m-2n),C(m+3,n-3,9)三点共线,则m+n= 0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com