
题目列表(包括答案和解析)
5.曲线y=x3-3x2+1在点(1,-1)处的切线方程为 ( A )
A.y=-3x+2 B.y=3x-4 C.y=-4x+3 D.y=4x-5
4.椭圆的短轴长为2,长轴是短轴的2倍,则椭圆的中心到其准线的距离是 ( D )
A.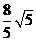 B.
B. C.
C. D.
D.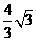
3.已知点A(1, -2, 11),B(4, 2, 3),C(6, -1, 4),则△ABC的形状是 ( C )
A.等腰三角形 B.正三角形 C.直角三角形 D.等腰直角三角形
3.若函数f(x)=2x2-1的图象两点(1,1)及(1+Δx,1+Δy),则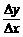 等于( C )
等于( C )
A.4 B.4x C.4+2Δx D.4+2Δx2
2.下列说法错误的是 ( C )
A.命题“若 则
则  ”的逆否命题为:“若
”的逆否命题为:“若 , 则
, 则 ”。
”。
B.“ ”是“
”是“ ”的充分不必要条件。
”的充分不必要条件。
C.若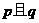 为假命题,则
为假命题,则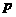 .
.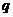 均为假命题。
均为假命题。
D.对于命题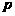 :
: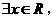 使得
使得 . 则
. 则
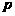 :
: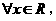 均有
均有 。
。
1.关于频率分布直方图,下列有关说法正确的是 ( D )
A.直方图的高表示取某数的频率。
B.直方图的高表示该组上的个体在样本中出现的频率。
C.直方图的高表示取某组上的个体在样本中出现的频数与组距的比值。
D.直方图的高表示取该组上的个体在样本中出现的频率与组距的比值。
20.(本小题满分14分)
设数列 的前
的前 项和为
项和为 ,
, .
.
(1)若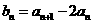 ,求
,求 ;
;
(2)若 ,求
,求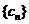 的前6项和
的前6项和 ;
;
(3)若 ,证明
,证明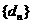 是等差数列.
是等差数列.
19.(本小题满分14分)
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6000m ,
 ∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
18.(本小题满分14分)
深圳某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
|
资金 |
每台空调或冰箱所需资金(百元) |
月资金供应数量 (百元) |
|
|
空调 |
冰箱 |
||
|
成本 |
30 |
20 |
300 |
|
工人工资 |
5 |
10 |
110 |
|
每台利润 |
6 |
8 |
|
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?最大利润是多少?
17.(本题满分14分)
△ABC的三个内角A、B、C对边分别是a, b,
c,且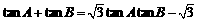 ,
,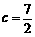 ,又△ABC的面积为
,又△ABC的面积为 .
.
求:(1)角C; (2)a+b的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com