
题目列表(包括答案和解析)
8.双曲线 的一条渐进线与直线
的一条渐进线与直线 垂直,则
垂直,则 。
。
7.以椭圆 的焦点为顶点,顶点为焦点的双曲线方程是___
___。
的焦点为顶点,顶点为焦点的双曲线方程是___
___。
6.椭圆 的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是__________。
的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是__________。
5.斜率为2的直线l被曲线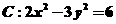 截得的弦长为4,则该弦的中点的坐标是___________________。
截得的弦长为4,则该弦的中点的坐标是___________________。
4.已知定点 ,动点
,动点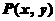 满足条件
满足条件 ,点Q与点P关于直线
,点Q与点P关于直线 对称,则点Q的轨迹是___
___。
对称,则点Q的轨迹是___
___。
3.直线l经过点 且与圆心在原点半径为1的圆面积相切,则直线l的方程是____ ___。
且与圆心在原点半径为1的圆面积相切,则直线l的方程是____ ___。
2.已知集合 ,集合
,集合 ,若
,若 ,则
,则 ____ ____。
____ ____。
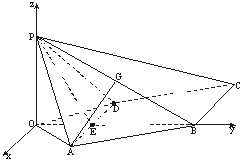
8.如图,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
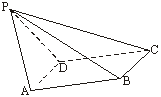
(Ⅰ)求点P到平面ABCD的距离;(Ⅱ)求面APB与面CPB所成二面角的大小.
(Ⅰ)解:如图,作PO⊥平面ABCD,垂足为点O.
连结OB、OA、OD,OB与AD交于点E,连结PE.
∵AD⊥PD,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD.
由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120 ,∠PEO=60
,∠PEO=60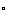 .由已知可求得PE=
.由已知可求得PE= ,
,
∴PO=PE·sin60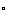 =
= ×
× =
= ,即点P到平面ABCD的距离为
,即点P到平面ABCD的距离为 .
.
(Ⅱ):如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.
P(0,0, ),B(0,
),B(0, ,0),PB中点G的坐标为(0,
,0),PB中点G的坐标为(0,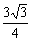 ,
, ),连结AG.
),连结AG.
又知A(1, ,0),C(-2,
,0),C(-2, ,0).由此得到:
,0).由此得到: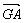 =(1,-
=(1,-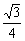 ,-
,- ),
),
 =(0,
=(0, ,-
,- ),
),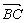 =(-2,0,0).于是有
=(-2,0,0).于是有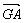 ·
· =0,
=0,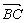 ·
· =0,
=0,
所以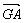 ⊥
⊥ ,
,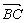 ⊥
⊥ .
.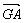 ,
,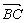 的夹角
的夹角 等于所求二面角的平面角,
等于所求二面角的平面角,
于是 cos =
= =-
=- ,
,
所以所求二面角的大小为π-arccos .
.
7、如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点。
(Ⅰ)求证:EF⊥平面PAB;(Ⅱ)设AB=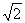 BC,求AC与平面AEF所成的角的大小。
BC,求AC与平面AEF所成的角的大小。
 证:以D为坐标原点,DA的长为单位,建立如图所示的直角坐标系.
证:以D为坐标原点,DA的长为单位,建立如图所示的直角坐标系.
(Ⅰ)证明:
设E(a,0,0)其中a>0,则C(2a,0,0),A(0,1,0)B(2a,1,0),P(0,0,1),F(a, ,
, ).
).

 =(0,
=(0, ,
, ),
),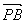 =(2a,1,-1),
=(2a,1,-1), =(2a,0,0)。
=(2a,0,0)。
 ·
·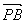 =0,∴EF⊥PB.
=0,∴EF⊥PB.
 ·
· =0,∴EF⊥AB
=0,∴EF⊥AB
又PB 平面PAB,AB
平面PAB,AB 平面PAB,PB∩AB=B.
平面PAB,PB∩AB=B.
∴EF⊥平面PAB.
(Ⅱ)解:由AB=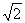 BC,得a=
BC,得a=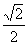 .
.
可得 =(
=(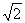 ,-1,0),
,-1,0),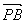 =(
=(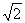 ,1,-1)
,1,-1)
cos< ·
·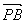 >=
>=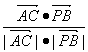 =
=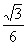 ,
,
异面直线AC、PB所成的角为arccos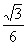 .
.
 =(
=(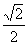 ,-
,- ,
, ).
).
∴ ·
·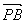 =0,PB⊥AF.
=0,PB⊥AF.
又PB⊥EF,EF、AF为平面AEF内两条相交直线,

即AC与平面AEF所成的角为arcsin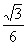 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com