
题目列表(包括答案和解析)
7、焦半径
(1)已知椭圆 上一点P到椭圆左焦点的距离为3,则点P到右准线的距离为____
(答:
上一点P到椭圆左焦点的距离为3,则点P到右准线的距离为____
(答: );
);
(2)已知抛物线方程为 ,若抛物线上一点到
,若抛物线上一点到 轴的距离等于5,则它到抛物线的焦点的距离等于____;
轴的距离等于5,则它到抛物线的焦点的距离等于____;
(3)若该抛物线上的点 到焦点的距离是4,则点
到焦点的距离是4,则点 的坐标为_____(答:
的坐标为_____(答: );(4)点P在椭圆
);(4)点P在椭圆 上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标为_______(答:
上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标为_______(答: );
);
(5)抛物线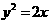 上的两点A、B到焦点的距离和是5,则线段AB的中点到
上的两点A、B到焦点的距离和是5,则线段AB的中点到 轴的距离为______(答:2);(6)椭圆
轴的距离为______(答:2);(6)椭圆 内有一点
内有一点 ,F为右焦点,在椭圆上有一点M,使
,F为右焦点,在椭圆上有一点M,使 之值最小,则点M的坐标为_______(答:
之值最小,则点M的坐标为_______(答: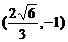 );
);
6.直线与圆锥曲线的位置关系:
(1)若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点,则k的取值范围是_______(答:(- ,-1));
,-1));
(2)直线y―kx―1=0与椭圆 恒有公共点,则m的取值范围是_______
恒有公共点,则m的取值范围是_______
(答:[1,5)∪(5,+∞));
(3)过双曲线 的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条 (答:3);
的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条 (答:3);
(2)过双曲线 =1外一点
=1外一点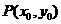 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。
(1)过点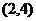 作直线与抛物线
作直线与抛物线 只有一个公共点,这样的直线有______(答:2);(2)过点(0,2)与双曲线
只有一个公共点,这样的直线有______(答:2);(2)过点(0,2)与双曲线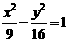 有且仅有一个公共点的直线的斜率的取值范围为______
(答:
有且仅有一个公共点的直线的斜率的取值范围为______
(答: );
);
(3)过双曲线 的右焦点作直线
的右焦点作直线 交双曲线于A、B两点,若
交双曲线于A、B两点,若 4,则满足条件的直线
4,则满足条件的直线 有____条
(答:3);
有____条
(答:3);
(4)对于抛物线C: ,我们称满足
,我们称满足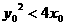 的点
的点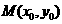 在抛物线的内部,若点
在抛物线的内部,若点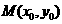 在抛物线的内部,则直线
在抛物线的内部,则直线 :
: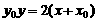 与抛物线C的位置关系是_______
(答:相离);
与抛物线C的位置关系是_______
(答:相离);
(5)过抛物线 的焦点
的焦点 作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是 、
、 ,则
,则 _______(答:1);
_______(答:1);
(6)设双曲线 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,设某直线
,设某直线 交其左支、右支和右准线分别于
交其左支、右支和右准线分别于 ,则
,则 和
和 的大小关系为___________(填大于、小于或等于) (答:等于);
的大小关系为___________(填大于、小于或等于) (答:等于);
(7)求椭圆 上的点到直线
上的点到直线 的最短距离(答:
的最短距离(答: );
);
(8)直线 与双曲线
与双曲线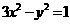 交于
交于 、
、 两点。①当
两点。①当 为何值时,
为何值时, 、
、 分别在双曲线的两支上?②当
分别在双曲线的两支上?②当 为何值时,以AB为直径的圆过坐标原点?
为何值时,以AB为直径的圆过坐标原点?
(答:① ;②
;② );
);
5、点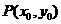 和椭圆
和椭圆 (
( )的关系:
)的关系:
4.圆锥曲线的几何性质:
(1)椭圆
(1)若椭圆 的离心率
的离心率 ,则
,则 的值是__ (答:3或
的值是__ (答:3或 );
);
(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__
(答: )
)
(2)双曲线
(1)双曲线的渐近线方程是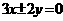 ,则该双曲线的离心率等于______
,则该双曲线的离心率等于______
(答: 或
或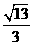 );
);
(2)双曲线 的离心率为
的离心率为 ,则
,则 = (答:4或
= (答:4或 );
);
(3)设双曲线 (a>0,b>0)中,离心率e∈[
(a>0,b>0)中,离心率e∈[ ,2],则两条渐近线夹角θ的取值范围是________
(答:
,2],则两条渐近线夹角θ的取值范围是________
(答: );
);
(3)抛物线;设 ,则抛物线
,则抛物线 的焦点坐标为________(答:
的焦点坐标为________(答: );
);
3.圆锥曲线焦点位置的判断:
椭圆:
已知方程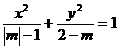 表示焦点在y轴上的椭圆,则m的取值范围是__
表示焦点在y轴上的椭圆,则m的取值范围是__
(答: )
)
2.圆锥曲线的标准方程
(1)椭圆:
(1)已知方程 表示椭圆,则
表示椭圆,则 的取值范围为____
的取值范围为____
(答: );
);
(2)若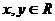 ,且
,且 ,则
,则 的最大值是____,
的最大值是____,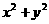 的最小值是___(答:
的最小值是___(答: )
)
(2)双曲线:
(1)双曲线的离心率等于 ,且与椭圆
,且与椭圆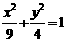 有公共焦点,则该双曲线的方程_______
(答:
有公共焦点,则该双曲线的方程_______
(答: );
);
(2)设中心在坐标原点 ,焦点
,焦点 、
、 在坐标轴上,离心率
在坐标轴上,离心率 的双曲线C过点
的双曲线C过点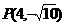 ,则C的方程为_______
(答:
,则C的方程为_______
(答: )
)
(3)抛物线:
1.圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:
(1)已知定点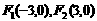 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.
,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.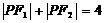 B.
B.
C. D.
D. (答:C);
(答:C);
(2)方程 表示的曲线是_____ (答:双曲线的左支)
表示的曲线是_____ (答:双曲线的左支)
(2)第二定义
已知点 及抛物线
及抛物线 上一动点P(x,y),则y+|PQ|的最小值是_____
上一动点P(x,y),则y+|PQ|的最小值是_____
(答:2)
22.如图,已知二面角 为60º,点A和点B分别在平面
为60º,点A和点B分别在平面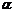 和平面
和平面 上,点C在棱
上,点C在棱
PQ上,∠ACP=∠BCP=30º,CA=CB=a,
⑴求证:AB⊥PQ;⑵求点B到平面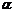 的距离;
的距离;
⑶设R是线段CA上的一点,直线BR与平面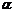 所成的角为45º,求线段CR的长度。
所成的角为45º,求线段CR的长度。

21.如图,在四棱椎P-ABCD中,底面ABCD是一直角梯形,∠BAD=90º,AD∥BC,
 AB=BC=a,AD=2a,PD与底面成30º角,PA⊥底面ABCD,
AB=BC=a,AD=2a,PD与底面成30º角,PA⊥底面ABCD,
⑴若AE⊥PD于E,求证:BE⊥PD;
⑵求异面直线AE、CD所成角的大小。
20.如图,△ABC和△DBC所在平面互相垂直,且AB=BC=BD,∠ABC=∠DBC=120º,
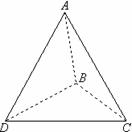 求:⑴A、D连线和平面DBC所成的角;⑵二面角A-BD-C的正切值。
求:⑴A、D连线和平面DBC所成的角;⑵二面角A-BD-C的正切值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com