
题目列表(包括答案和解析)
6.设 是直线,
是直线,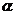 、
、 是平面,给出下列三个条件:①
是平面,给出下列三个条件:① ;②
;②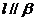 ;③
;③
以其中两个作为题设,另一个作为结论,则可构成三个命题,这三个命题中正确的个数为
A.3个 B.2个 C.1个 D.0个
5.设 、
、 是两条不同直线,
是两条不同直线,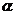 、
、 是两个不同平面,则下列命题
是两个不同平面,则下列命题
① ②
②
③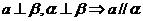 ④
④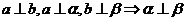
其中正确的命题的个数是
A.0个 B.1个 C.2个 D.3个
4.在四棱锥 中,为了推出
中,为了推出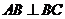 ,需从下列条件:①
,需从下列条件:① 面
面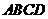 ;
;
② ;③
;③ 面
面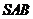 ;④
;④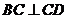 中选出部分条件,这些条件可能是
中选出部分条件,这些条件可能是
A.②③ B.①④ C.②④ D.③④
2.下面几个命题:
①“直线 直线
直线 ”的充要条件是“
”的充要条件是“ 平行于
平行于 所在的平面”;
所在的平面”;
②“直线 平面
平面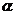 内所在直线”的充要条件是“
内所在直线”的充要条件是“
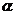 ”
”
③“直线 、
、 为异面直线”的充分不必要条件是“直线
为异面直线”的充分不必要条件是“直线 、
、 不相交”;
不相交”;
④“平面 平面
平面 ”的必要不充分条件是“
”的必要不充分条件是“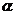 内存在不共线的三点到
内存在不共线的三点到 的距离相等”。
的距离相等”。
其中正确的命题是
A.①② B.②③ C.③④ D.②④
3若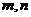 是两条异面直线,则总存在一个确定的平面
是两条异面直线,则总存在一个确定的平面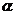 ,满足
,满足
A. ,
, B.
B.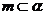 ,
, C.
C.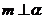 ,
, D.
D.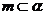 ,
,
1.已知相交直线 都在平面
都在平面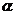 内,且都不在平面
内,且都不在平面 内,若
内,若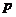 :
: 中至少有一条与
中至少有一条与 相交;
相交; :
: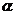 与
与 相交,则
相交,则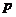 是
是 的
的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分也不必要条件
22.(14分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上,其右焦点到直线x-y+2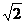 =0的距离为3。(1)求椭圆的方程;(2)椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N。当|AM|=|AN|时,求m取值范围。
=0的距离为3。(1)求椭圆的方程;(2)椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N。当|AM|=|AN|时,求m取值范围。
21.(14分)如图,四棱锥S-ABCD的底面ABCD是正方形,
SA⊥底面ABCD,E是SC上的一点,
(1)求证:平面EBD⊥平面SAC;
(2)若SA=4,AB=2,求点A到平面SBD的距离;
 (3)当
(3)当 的值为多少时,二面角B-SC-D的大小为
的值为多少时,二面角B-SC-D的大小为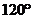 ?
?
20.(12分)高三(1)班、高三(2)每班已选出3名学生组成代表队,进行乒乓球对抗赛,比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,不得参加两盘单打比赛;③先胜两盘的队获胜,比赛结束.已知每盘比赛双方胜出的概率均为
(Ⅰ)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率是多少?
(Ⅲ)高三(1)班代表队至少胜一盘的概率为多少?
19.(12分)已知圆C1:(x+5)2+y2=49,圆C2:(x-5)2+y2=1,动圆M与圆C1和圆C2都外切。求动圆的圆心M的轨是方程。
18. 求由约束条件 确定的平面区域的面积
确定的平面区域的面积 和周长
和周长 .(12分)
.(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com