
题目列表(包括答案和解析)
3.中心在原点,焦点坐标为(0, ±5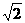 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为 ,则椭圆方程为 ( )
,则椭圆方程为 ( )
A. +
+ =1 B.
=1 B. +
+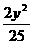 =1 C.
=1 C. +
+ =1 D.
=1 D. +
+ =1
=1
2.设双曲线 =1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为
=1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为 c,则双曲线的离心率为 ( )
c,则双曲线的离心率为 ( )
A.2 B. C.
C. D.
D.
1.x= 表示的曲线是 ( )
表示的曲线是 ( )
A.双曲线 B.椭圆
C.双曲线的一部分 D.椭圆的一部分
20.(14分)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形且∠C1CB=∠C1CD=∠BCD=60°.
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=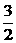 ,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
(3)当 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
19.(14分)如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求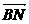 的长;
的长;
(2)求cos< >的值;
>的值;
(3)求证:A1B⊥C1M.

18.(12分)四棱锥P-ABCD中,底面ABCD是一个平行四边形, ={2,-1,-4},
={2,-1,-4}, ={4,2,0},
={4,2,0}, ={-1,2,-1}.
={-1,2,-1}.
(1)求证:PA⊥底面ABCD;
(2)求四棱锥P-ABCD的体积;
(3)对于向量 ={x1,y1,z1},
={x1,y1,z1}, ={x2,y2,z2},
={x2,y2,z2},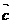 ={x3,y3,z3},定义一种运算:
={x3,y3,z3},定义一种运算:
( ×
× )·
)·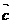 =x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算(
=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算( ×
× )·
)· 的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并由此猜想向量这一运算(
的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并由此猜想向量这一运算( ×
× )·
)· 的绝对值的几何意义..
的绝对值的几何意义..
17.(12分)若四面体对应棱的中点间的距离都相等,证明这个四面体的对棱两两垂直.
16.(12分)如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是( ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
 (1)求向量
(1)求向量 的坐标;
的坐标;
(2)设向量 和
和 的夹角为θ,求cosθ的值
的夹角为θ,求cosθ的值
15.(12分)如图,已知正方体 的棱长为a,M为
的棱长为a,M为 的中点,点N在
的中点,点N在 '上,且
'上,且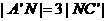 ,试求MN的长.
,试求MN的长.
14.已知向量 ,
, ,若
,若 成1200的角,则k= .
成1200的角,则k= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com