13.出题意图：考查导数的几何意义.

　 分析：求平行直线的切线，实质上是求函数在哪一点的导数为直线的斜率4.

解：

令，则即在(2，5)处的切线平行于直线　

讲评：函数处的导数的几何意义是曲线在点处的切线的斜率.

　　　 14出题意图：考查导数的物理意义.

分析：根据时间求出两次时间对应的路程，从而求出路程的变化量；进而求出平均速度，根据该点导数求出瞬时速度.

　　　 解：(1)

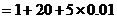
　　　　　　　　 (m)

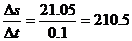　　　　　　　 (m/s).

　　　　　 (2)由导数的定义，在t=20的瞬时速度为

　　　　　　　　 =

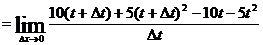
　　　　　　　　 =10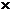20+10

=210(m/s).

　　　 答：

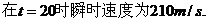
　　　　 讲评：平均速度和瞬时速度是两个完全不同的概念，平均速度是相对一段时间来说的，瞬时速度是相对一时刻来说的，但是平均速度与瞬时速度由有着密切的联系，瞬时速度是在平均速度的时间接近于0的时候的值.　

3. 求极限.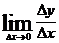

　　 (2)求函数在某一点的导数方法有两种，一种直接求出函数在该点的导数.另一种是求出导函数，再求导数在该点的函数值.

2. 求比.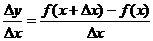

1．求函数的改变量.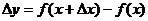

12.出题意图：考察函数导数的定义.

　 分析：先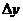求，再求.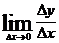

　 解：

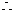
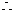
讲评：(1)用定义求导数必须严格按照三个步骤进行.

11.(1，1)，(-1，-1)提示：切线的斜率等于3，即在该点函数的导数为3，故根据定义求出函数导数，令=1，可求得点的横坐标.

三解答：

10. 4m/s 提示：注意带单位，瞬时速度即函数在某点的导数，故求该点导数即可.

9.　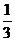 　提示：根据题意得，

8.B 提示：方法1：要求直线方程，就要求直线的斜率，即求函数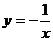在点()的导数，然后利用直线的方程的点斜式求解.

　　　　 方法2：代入点()可以采用排除法.

二填空：

7.B 提示：要求曲线在某点的切线的倾斜角，就要求在该点的切线的斜率，即求函数在点()处的导数.然后利用三角函数知识求解.