
题目列表(包括答案和解析)
3. 在第1、3、4、路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车),有一位乘客等候第4路或第8路汽车.假定当时各5、8路汽车首先到站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于
A.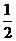 B.
B. 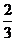 C.
C.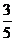 D.
D.
2. 从分别写有A、B、C、D、E的5张卡片中,任取2张,这2张卡片上的字母恰好是按字母顺序相邻的概率为
A. B.
B. C.
C.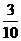 D.
D.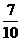
1.一枚硬币连掷3次,只有一次出现正面的概率是
A.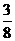 B.
B.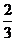 C.
C.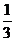 D.
D.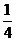
19.(本小题满分12分)在△ABC中,已知B(-2,0)、C(2,0),AD⊥BC于点D,△ABC的垂心为H,且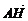 =
=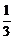
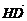 .
.
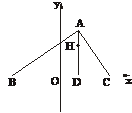
(1)求点H(x,y)的轨迹G的方程;
(2)已知P(-1,0)、Q(1,0),M是曲线G上的一点,那么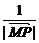 ,
,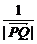 ,
,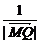 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
(1)解:∵H点坐标为(x,y),则D点坐标为(x,0),
由定比分点坐标公式可知,A点的坐标为(x,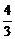 y).
y).
∴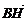 =(x+2,y),
=(x+2,y),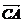 =(x-2,
=(x-2,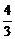 y).
y).
由BH⊥CA知x2-4+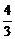 y2=0,即
y2=0,即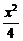 +
+ 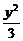 =1,
=1,
∴G的方程为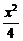 +
+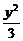 =1(y≠0).
=1(y≠0).
(2)解法一:显然P、Q恰好为G的两个焦点,
∴|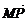 |+|
|+|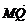 |=4,|
|=4,|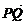 |=2.
|=2.
若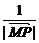 ,
,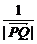 ,
,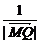 成等差数列,则
成等差数列,则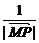 +
+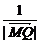 =
=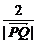 =1.
=1.
∴|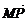 |·|
|·|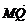 |=|
|=| 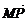 |+|
|+|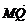 |=4.
|=4.
由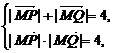 可得|
可得|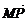 |=|
|=|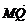 |=2,
|=2,
∴M点为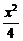 +
+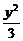 =1的短轴端点.
=1的短轴端点.
∴当M点的坐标为(0, 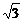 )或(0,-
)或(0,-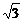 )时,
)时,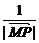 ,
,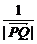 ,
,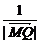 成等差数列.
成等差数列.
解法二:设M点的坐标为(x,y),
显然P、Q恰好为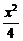 +
+ 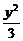 =1的两个焦点,
=1的两个焦点,
∴|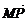 |+|
|+|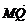 |=4,|
|=4,| 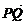 |=2.
|=2.
∵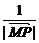 ,
,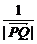 ,
,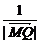 成等差数列,
成等差数列,
∴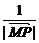 +
+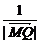 =
=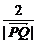 =1.
=1.
由椭圆第二定义可得|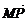 |=a+ex,|
|=a+ex,|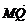 |=a-ex,
|=a-ex,
∴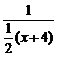 +
+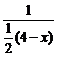 =1.解得x=0.
=1.解得x=0.
∴M点的坐标为(0, 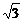 )或(0,-
)或(0,-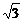 ).
).
∴当M点的坐标为(0, 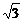 )或(0,-
)或(0,-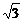 )时,
)时,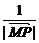 ,
,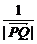 ,
,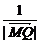 成等差数列.
成等差数列.
18.(本小题满分12分)如下图,双曲线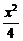 -
-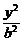 =1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
=1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
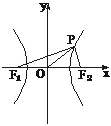
解:∵|PF1|、|F1F2|、|PF2|成等差数列,
∴|PF1|+|PF2|=2|F1F2|=4c.
又|PF1|-|PF2|=2a=4,
∴|PF1|=2c+2,|PF2|=2c-2.
根据中线定理有|PF1|2+|PF2|2=2(|PO|2+|F1O|2)<2(52+c2),
∴(2c+2)2+(2c-2)2<2(52+c2).
∴8c2+8<50+2c2.
∴c2<7,
即4+b2<7.∴b2<3.又b∈N*,∴b=1.
∴所求双曲线方程为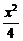 -y2=1.
-y2=1.
17.(本小题满分12分)求以椭圆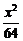 +
+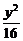 =1的顶点为焦点,且一条渐近线的倾斜角为
=1的顶点为焦点,且一条渐近线的倾斜角为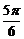 的双曲线方程.
的双曲线方程.
分析:已知渐近线方程为bx±ay=0,中心在原点,求双曲线的方程.可设双曲线方程为 b2x2-a2y2=λ(λ≠0),根据其他条件,确定λ的正负.
解:椭圆的顶点坐标为(±8,0)、(0,±4).
∵双曲线渐近线方程为x±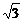 y=0,
y=0,
则可设双曲线方程为x2-3y2=k(k≠0),
即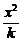 -
-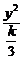 =1.
=1.
若以(±8,0)为焦点,则k+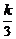 =64,得k=48,双曲线方程为
=64,得k=48,双曲线方程为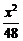 -
-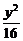 =1;
=1;
若以(0,±4)为焦点,则-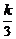 -k=16,得k=-12,双曲线方程为
-k=16,得k=-12,双曲线方程为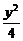 -
- =1.
=1.
16.(本小题满分10分)已知椭圆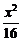 +
+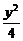 =1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
=1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.

解:如图,设弦与椭圆的两交点坐标为A(x1,y1)、B(x2,y2).又P(2,1),
 ∴
∴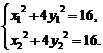
①-②得(x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,
∴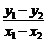 =-
=-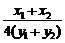 =-
=-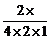 =-
=-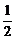 =kAB.
=kAB.
∴lAB的方程为y-1=-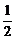 (x-2).
(x-2).
15.(本小题满分8分)设椭圆的中心为坐标原点,它在x轴上的一个焦点与短轴两端点连成60°的角,两准线间的距离等于8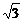 ,求椭圆方程.
,求椭圆方程.
解:依题意,设所求椭圆方程为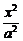 +
+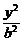 =1,
=1,
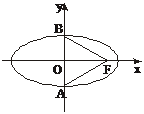
∵椭圆右焦点F(c,0)与短轴两端点A、B连成60°的角,
如图,则∠AFB=60°,△AFB为等边三角形,
于是有a=2b. ①
又由两准线间的距离等于8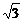 ,得
,得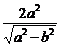 =8
=8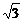 . ②
. ②
联立①②两方程,解得a=6,b=3.
故所求椭圆方程为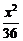 +
+ 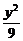 =1.
=1.
14.方程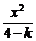 +
+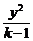 =1表示的曲线为C,给出下列四个命题:
=1表示的曲线为C,给出下列四个命题:
①曲线C不可能是圆;
②若1<k<4,则曲线C为椭圆;
③若曲线C为双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<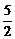 .
.
其中正确的命题是__________.
解析:当4-k=k-1,即k=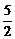 时表示圆,否定命题①,显然k=
时表示圆,否定命题①,显然k=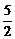 ∈(1,4),
∈(1,4),
∴否定命题②;若曲线C为双曲线,则有(4-k)(k-1)<0,即4<k或k<1,故命题③正确;若曲线C表示焦点在x轴上的椭圆,则4-k>k-1>0,解得1<k<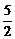 ,说明命题④正确.
,说明命题④正确.
答案:③④
13.经过点M(10, 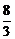 ),渐近线方程为y=±
),渐近线方程为y=±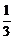 x的双曲线方程为__________.
x的双曲线方程为__________.
分析:本题考查依据条件求双曲线的方程.
解:设双曲线的方程为(x-3y)(x+3y)=m(m∈R,且m≠0),
因双曲线过点M(10,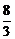 ),所以有(10-3×
),所以有(10-3×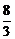 )(10+3×
)(10+3×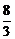 )=m,得m=36.
)=m,得m=36.
所以双曲线方程为x2-9y2=36,即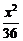 -
-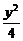 =1.
=1.
答案: 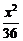 -
-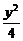 =1
=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com