
题目列表(包括答案和解析)
5.(如右图)正方体ABCD-A1B1C1D1中,AC与B1D所成的
角为( )
A、 B、
B、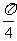 C、
C、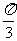 D、
D、
4.下面叙述正确的是( )
A.过平面外一点只能作一条直线与这个平面平行
B.过直线外一点只能作一个平面与这条直线平行
C.过平面外一点只能作一个平面与这个平面垂直
D.过直线外一点只能作一个平面与这条直线垂直
3.已知P为△ABC所在平面α外一点,PA=PB=PC,则P点在平面α内的射影一定是△ABC的 ( )
 A、内心 B、外心 C、垂心 D、重心
A、内心 B、外心 C、垂心 D、重心
2.以下四个结论:① 若a α, b
α, b β,则a, b为异面直线;
β,则a, b为异面直线;
② 若a α, b
α, b α,则a, b为异面直线;
α,则a, b为异面直线;
③ 没有公共点的两条直线是平行直线;
④ 两条不平行的直线就一定相交。其中正确答案的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
1.点A在直线l上,l在平面α外,用符号表示正确的是 ( )
(A)A∈l,l α
α (B)A∈l,l
(B)A∈l,l α (C)A
α (C)A l,l
l,l α (D)A
α (D)A l,l∈α
l,l∈α
15, (满分8分)某医院有内科医生6名,外科医生4名,现要选派5名参加赈灾医
疗队。
(1)某内科医生必须参加,某外科医生不能参加,有多少种?(4分)
(2)至少有一名内科医生和至少有一名外科医生参加有多少种选?(4分)
16, (满分9分)
一盒中放有除颜色不同外,其余完全相同的黑球和白球,其中黑球2个,白球3个。
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率;(4分)
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率 (5分)
17, (满分9分) 数列 满足
满足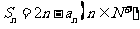
(1)计算 ,并由此猜想通项公式;(4分)
,并由此猜想通项公式;(4分)
(2)用数学归纳法证明①中的猜想。(5分)

 18, (满分9分) 已知tana,tanb是关于x的一元二次方程x2+px+2=0的两实根.
18, (满分9分) 已知tana,tanb是关于x的一元二次方程x2+px+2=0的两实根.
(1)求证: ;(4分)(2)求证:.
;(4分)(2)求证:.  (5分)
(5分)
(要求用综合法) (要求用分析法)
19, (满分9分)已知函数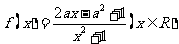 ,其中
,其中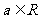
(1)当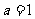 时,求曲线
时,求曲线 在点
在点 处的切线方程;(3分)
处的切线方程;(3分)
(2)当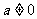 时,求函数
时,求函数 的单调区间与极大值。(6分)
的单调区间与极大值。(6分)
14、① ; ② ; ③ ;
13、 ;
11、 ; 12、 ;
21.(4+4+5=13分)已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角
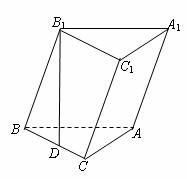 为α (0°<α<90°),点
为α (0°<α<90°),点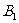 在底面上的射影
在底面上的射影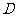 落在
落在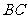 上.
上.
(1)求证:AC⊥平面BB1C1C;
(2)若AB1⊥BC1,D为BC的中点,求α ;
(3)若α = arccos ,且AC=BC=AA1时,求二面角C1-AB-C的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com