
题目列表(包括答案和解析)
3、如果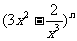 的展开式中含有非零常数,则正整数n的最小值为( )
的展开式中含有非零常数,则正整数n的最小值为( )
A、3 B、5 C、6 D、10
1. 已知 的二项展开式的第7项为
的二项展开式的第7项为 ,则x的值等于( )
,则x的值等于( )
A.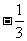 B.
B. C.
C.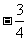 D.
D.
2 (普通班)若n为正奇数,则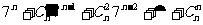 被9除所得余数是( )
被9除所得余数是( )
A、0 B、3 C、-2 D、8
(重点班)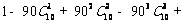 …
… 除以88的余数是 ( )
除以88的余数是 ( )
A. -87 B.  1
C.1
D.87
1
C.1
D.87
22.解 ⑴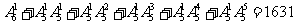 个
个
⑵要求是5位数,因此6个数中选5个,首位不能是0,个位必须是偶数,分为三种取法
①5位数中无0 个位有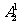 种取法,其余有
种取法,其余有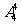 ,即共有
,即共有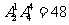 个
个
②5位数中有0 ⅰ 0在个位,共有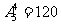 个,ⅱ 0不在各位
个,ⅱ 0不在各位 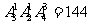
∴共有 48+120+144=312个
⑶首位以 3,4,5开头的5为数都符合要求共计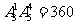 ,
,
其次以25开头的数有 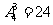 ,
,
以245开头的数有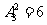 ,
,
以243开头的数有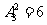 ,有4个数比24305大
,有4个数比24305大
∴共有360+24+6+4=394 个
21. 解:(1)除 、
、 选出外,从其它10个人中再选3人,共有的选法种数为
选出外,从其它10个人中再选3人,共有的选法种数为 ,
,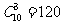 (种).
(种).
(2)去掉 、
、 ,从其它10人中任选5人,共有的选法种数为:
,从其它10人中任选5人,共有的选法种数为: (种).
(种).
(3)按 、
、 的选取情况进行分类:
的选取情况进行分类: 、
、 全不选的方法数为
全不选的方法数为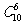 ,
, 、
、 选1人的方法数为
选1人的方法数为 ,共有选法
,共有选法 (种).
(种).
本小题的另一解法:从12人中选5人的选法中去掉 、
、 全选的情况,所有选法只有
全选的情况,所有选法只有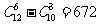 (种).
(种).
方法一:按女同学的选取情况分类:
选2名女同学、3名男同学;选3名女同学2名男同学;选4名女同学1名男同学;选5名女同学.所有选法数为:
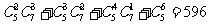 (种).
(种).
方法二:从反面考虑,用间接方法,去掉女同学不选或选1人的情况,所有方法总数为: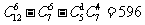 (种).
(种).
(5)选出一个男生担任体育班委,再选出1名女生担任文娱班委,剩下的10人中任取3人担任其它3个班委.用分步计数原理可得到所有方法总数为: (种).
(种).
20、解:⑴、将4个球分成三类情况:
①、取4个球,没有白球有 种……………………………………………2分
种……………………………………………2分
②、取3个红球1个白球有 种………………………………………4分
种………………………………………4分
③、取2个红球2个白球有 种
种
∴取法共有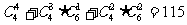 种……………………………6分
种……………………………6分
⑵、设取 个红球,
个红球,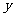 个白球,则
个白球,则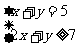
 ,
,
∴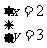 或
或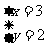 或
或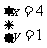 ……………………………………………………8分
……………………………………………………8分
∴符合题意的取法种数有 种……………12分
种……………12分
19.解(1)(特殊元素优先排)先安排甲乙二人到中间的6个位置中的两个,有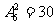 种,
种,
其余的6个人全排列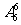 种,所以共计:
种,所以共计: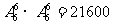 种排法.
种排法.
(2)(捆绑法)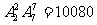 种.
种.
(3)(插入法、捆绑法)余下的六人中任选两人放在甲乙二人中间,有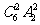 种,甲乙二人全排,有
种,甲乙二人全排,有 种,然后把这四人“捆绑”与其他四人排队,有
种,然后把这四人“捆绑”与其他四人排队,有 种, ∴共有
种, ∴共有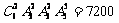 种.
种.
(4)(定序相除法)8个人全排列有 种,甲乙丙三人有
种,甲乙丙三人有 种,乙丙二人有
种,乙丙二人有 种,
种,
∴共有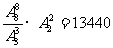 种.
种.
18. 解:(1). 无重复数字的三位数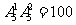 个.
个.
(2). 无重复数字的三位奇数 个.
个.
(3). 大于3012且无重复数字的四位数 个.
个.
17. 解:(1). 从口袋内取出3个球的取法共有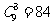 种.
种.
(2). 从口袋内取出3个球,使其中恰有1个黑球的取法共有 种.
种.
(3). 从口袋内取出3个球,使其中至少有1个黑球的取法共有 种.
种.
22.(9分)由0~5这六个数;①可组成没有重复数字的数多少个?②可组成没有重复数字的5位数中偶数多少个?③可组成没有重复数字的5位数中比24305大的数有多少个?
13 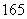
 14、
14、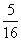 15.59___ 16. 16
15.59___ 16. 16
20、(9分)一个口袋内有4个不同的红球,6个不同的白球。⑴、从中任取4个球,红球的个数不比白球少的取法有多少种?⑵、若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
21(9分)、从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(1) 、
、 必须当选;(2)
必须当选;(2) 、
、 都不当选;(3)
都不当选;(3) 、
、 不全当选;(4)至少有2名女生当选;(5)选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
不全当选;(4)至少有2名女生当选;(5)选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com