15。理科20

14(普通班).

14．(重点班)解：10个空位加4个挡板位，共有14个放挡板的位置，有种方法。

13.2

22．已知数列{a _n}是首项为a、公比为q的等比数列，

(1) 化简 　以及 ；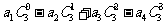

(2)根据①的结果概括出关于正整数n的一个结论，并加以证明．

21．在的展开式中，前三项系数的绝对值成等差数列，

(1)　 求展开式中二项式系数最大的项；　　

(2)　 展开式中是否含有常数项？若有，请求出来；若没有，说明理由．

20．(本小题满分8分)已知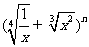 展开式中的倒数第三项的系数为45，

求：⑴含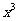的项；⑵系数最大的项．

18　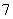 个排成一排，在下列情况下，各有多少种不同排法？

(1)甲排头，(2)甲不排头，也不排尾，(3)甲、乙、丙三人必须在一起，(4)甲不排头，乙不排当中(5)甲、乙、丙三人两两不相邻，(6)甲、乙之间有且只有两人。

19．在二项式的展开式中，前三项系数的绝对值成等差数列．

求展开式的第四项；　　

求展开式的常数项；

求展开式中各项的系数和。

17．从装有个球(其中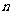个白球，1个黑球)的口袋中取出个球,共有种取法。在这种取法中，可以分成两类：一类是取出的个球全部为白球，一类是取出的个白球和1个黑球，共有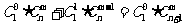，即有等式：成立。试根据上述思想化简下列式子：　　 　　　　　。。

16.求和：m!+++…+=__________.

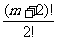15、在(1+x)⁵+(1+x)⁶+(1+x)⁷的展开式中，含x⁴项的系数是通项公式为a_n=3n-5的数列的第_____项。