
题目列表(包括答案和解析)
11、(1)略证:取PD的中点H,连接AH,
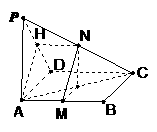

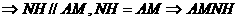 为平行四边形
为平行四边形
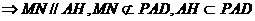

(2) 解:
连接AC并取其中点为O,连接OM、ON,则OM平行且等于BC的一半,ON平行且等于PA的一半,所以 就是异面直线
就是异面直线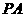 与
与 所成
所成
的角,由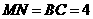 ,
, 得,OM=2,ON=
得,OM=2,ON=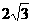

所以 ,即异面直线
,即异面直线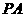 与
与 成
成 的角
的角
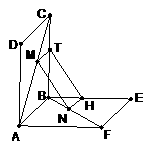
9、PQ与a异面. 10、平行;AC∥ 平面BA1C1
7、无数; 无数. 8、既不充分也不必要.
12.解:A a,∴A、a确定一个平面,设为β.
a,∴A、a确定一个平面,设为β.
∵B∈a,∴B∈β,又A∈β,∴AB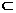 β
β
同理AC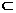 β,AD
β,AD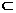 β
β
∵点A与直线a在α的异侧. ∴β与α相交,∴面ABD与面α相交,交线为EG
∵BD∥α,BD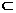 面BAD,面BAD∩α=EG ∴BD∥EG,∴△AEG∽△ABD.
面BAD,面BAD∩α=EG ∴BD∥EG,∴△AEG∽△ABD.
∴ (相似三角形对应线段成比例) ∴EG=
(相似三角形对应线段成比例) ∴EG=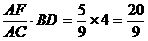 .
.
09033
1-6、ACBDDA
11、略证:
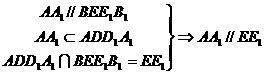
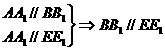

10、E、F分别是AB、BC的中点



7、平行或异面 8、平行 9、D1C、B1C、D1B1
6、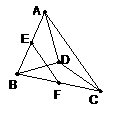 (1)√ (2)
×? (3)
×? (4)
√
(1)√ (2)
×? (3)
×? (4)
√
14. AD∶DB=AE∶EC
AD∶DB=AE∶EC
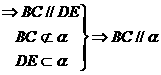

09032
1-5、DDADC
13. 求证:AC∥平面EFG,BD∥平面EFG.
证明:连结AC、BD、EF、FG、EG.
在△ABC中,∵E、F分别是AB、BC的中点 ∴AC∥EF
又EF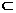 面EFG,AC
面EFG,AC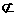 面EFG
面EFG
∴AC∥面EFG
同理可证BD∥面EFG.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com