
题目列表(包括答案和解析)
5.已知(2x2+4x+3)6=a0+a1(x+1)2+a2(x+1)4+…+a6(x+1)12,则a0+a2+a4+a6的值为 .
4.满足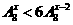 的实数
的实数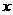 =
.
=
.
3. 下面给出了关于复数的四种类比推理: ①复数的加减法运算可以类比多项式的加减法运算法则;②由向量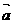 的性质|
的性质|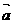 |2=
|2=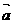 2 类比得到复数z的性质|z|2=z2;③方程
2 类比得到复数z的性质|z|2=z2;③方程 有两个不同实数根的条件是
有两个不同实数根的条件是 可以类比得到:方程
可以类比得到:方程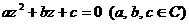 有两个不同复数根的条件是
有两个不同复数根的条件是 ;④由向量加法的几何意义可以类比得到复数加法的几何意义.其中类比错误的是
.
;④由向量加法的几何意义可以类比得到复数加法的几何意义.其中类比错误的是
.
2.若随机变量ξ的分布列为:P(ξ=k)= 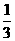 ,k=1,2,3,则V(3ξ+5)= .
,k=1,2,3,则V(3ξ+5)= .
1.  的值为 .
的值为 .
20.(本题18分)某同学做了一个数字信号模拟传送器,经过10个环节,把由数字0,1构成的数字信号由发生端传到接受端。已知每一个环节会把1错转为0的概率为0.3,把0错转为1的概率为0.2,若发出的数字信号中共有10000个1,5000个0.
问:(1)从第1个环节转出的信号中0,1各有多少个?
(2)最终接受端收到的信号中0,1个数各是多少?(精确到十位)
(3)该同学为了完善自己的仪器,决定在接受端前加一个修正器,把得到的1和0分别以一定的概率转换为0和1,则概率分别等于多少时,才能在理论上保证最终接受到的0和1的个数与发出的信号同.
19.数列 满足:
满足: =1,
=1,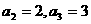 ,
, (
(
 )
)
(1)求实数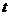 的值(2)求
的值(2)求 的值,根据
的值,根据 ,
,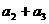 ,
, 的值,猜想
的值,猜想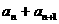 与
与 的关系式,并证明你的猜想
的关系式,并证明你的猜想
18.一袋中有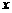 (
( )个红球,3个黑球和2个白球,现从中任取2个球.
)个红球,3个黑球和2个白球,现从中任取2个球.
(Ⅰ)当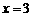 时,求取出的2个球球颜色都相同的事件的概率;
时,求取出的2个球球颜色都相同的事件的概率;
(Ⅱ)当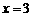 时,设
时,设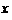 表示取出的2个球中红球的个数,求
表示取出的2个球中红球的个数,求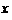 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅲ)如果取出的2个球颜色不相同的事件概率小于 ,求
,求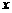 的最小值.
的最小值.
17.从5名女同学和4名男同学中选出4人参加演讲比赛,分别按下列要求,各有多少种不同选法?⑴男、女同学各2名; ⑵男、女同学分别至少有1名;
⑶在(2)的前提下,男同学甲与女同学乙不能同时选出.
16.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
|
推销员编号 |
1 |
2 |
3 |
4 |
5 |
工作年限 /年 /年 |
3 |
5 |
6 |
7 |
9 |
推销金额 /万元 /万元 |
2 |
3 |
3 |
4 |
5 |
(Ⅰ)求年推销金额 与工作年限x之间的相关系数;
与工作年限x之间的相关系数;
(Ⅱ)求年推销金额 关于工作年限
关于工作年限 的线性回归方程;
的线性回归方程;
(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
(参考数据:;由检验水平0.01及 ,查表得
,查表得 .)
.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com